题目内容
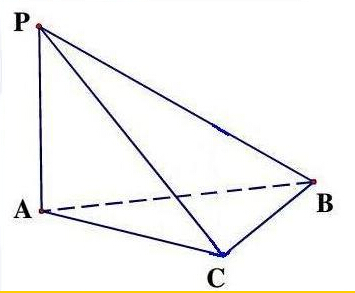如图所示，在四面体P-ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=2| 34 |
考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：由PA2+AC2=36+64=100=PC2，据勾股定理可证PA⊥AC，同理可证PA⊥AB，PC⊥BC，BC⊥AC，从而根据直线与平面垂直的判定定理即可证明．
解答：
证明：∵PA2+AC2=36+64=100=PC2，∴PA⊥AC
∵PA2+AB2=36+100=136=PB2，∴PA⊥AB
∵AB∩AC=A
∴PA⊥平面ABC
∵PC2+BC2=100+36=136=PB2，∴PC⊥BC
∵BC2+AC2=36+64=100=AB2，∴BC⊥AC
∵PC∩AC=C
∴BC⊥平面PAC．
∵PA2+AB2=36+100=136=PB2，∴PA⊥AB
∵AB∩AC=A
∴PA⊥平面ABC
∵PC2+BC2=100+36=136=PB2，∴PC⊥BC
∵BC2+AC2=36+64=100=AB2，∴BC⊥AC
∵PC∩AC=C
∴BC⊥平面PAC．
点评：本题考查了直线与平面垂直的判定，勾股定理的应用，属于基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知-
＜θ＜
，sinθ+cosθ=a，其中0＜a＜1，则tanθ可能是（ ）
| π |
| 2 |
| π |
| 2 |
| A、-2 | ||
B、-
| ||
C、2或-
| ||
D、-1或-
|
椭圆两焦点为F1（-4，0）、F2（4，0），P在椭圆上，若△PF1F2的面积的最大值为12，则椭圆方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将长、宽分别为4和3的长方形ABCD沿对角线AC折起，得到四面体A-BCD，则四面体A-BCD的外接球的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
