题目内容
已知函数f(x),x∈R,对任意x1、x2∈R,均有f(x1+x2)=f(x1)+f(x2),又x>0时,f(x)<0,f(1)=a,试判断函数f(x)在[-3,3]上是否有最值.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据条件,x1=x2=0得到f(0)=0,x1+x2=0,得到f(-x1)=-f(x1),再令x1<x2,由条件得到f(x)在R上是单调递减,从而函数f(x)在[-3,3]上是单调递减的,得到f(-3)为最大值,f(3)为最小值,讨论a=0,a<0,a>0判断有无最值即可.
解答:
解:∵对任意x1、x2∈R,均有f(x1+x2)=f(x1)+f(x2),
∴令x1=x2=0,则f(0)=2f(0),f(0)=0,
∴令x1+x2=0,则f(0)=f(x1)+f(-x1),即f(-x1)=-f(x1),
令x1<x2,则x2-x1>0,
∵x>0时,f(x)<0,∴f(x2-x1)<0,即f(x2)-f(x1)<0,
∴f(x)在R上是单调递减,
∵f(1)=a,∴f(2)=2f(1)=2a,f(3)=f(1)+f(2)=3a,f(-3)=-3a,
∴函数f(x)在[-3,3]上是单调递减的,
∴当a≥0时,函数无最值;当a<0时,f(-3)为最大值,且为-3a;f(3)为最小值,且为3a.
∴令x1=x2=0,则f(0)=2f(0),f(0)=0,
∴令x1+x2=0,则f(0)=f(x1)+f(-x1),即f(-x1)=-f(x1),
令x1<x2,则x2-x1>0,
∵x>0时,f(x)<0,∴f(x2-x1)<0,即f(x2)-f(x1)<0,
∴f(x)在R上是单调递减,
∵f(1)=a,∴f(2)=2f(1)=2a,f(3)=f(1)+f(2)=3a,f(-3)=-3a,
∴函数f(x)在[-3,3]上是单调递减的,
∴当a≥0时,函数无最值;当a<0时,f(-3)为最大值,且为-3a;f(3)为最小值,且为3a.
点评:本题主要考查解决抽象函数的常用方法:赋值,同时考查函数的单调性和应用,求函数的最值.属于中档题.

练习册系列答案
相关题目
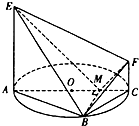 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.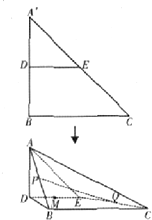 如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.
如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.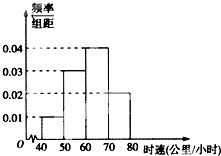 已知某一段公路限速60公里/小时,现抽取200辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这200辆汽车中在该路段没有超速的有
已知某一段公路限速60公里/小时,现抽取200辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这200辆汽车中在该路段没有超速的有