题目内容
已知曲线W:
+|y|=1,则曲线W上的点到原点距离的取值范围是( )
| x2+y2 |
A、[
| ||||
B、[2-
| ||||
C、[2-
| ||||
D、[1,
|
考点:两点间距离公式的应用
专题:计算题,圆锥曲线的定义、性质与方程
分析:化简方程
+|y|=1,得到x2=1-2|y|,作出曲线W的图形,通过图象观察,即可得到到原点距离的最值,进而得到范围.
| x2+y2 |
解答:
 解:
解:
+|y|=1即为
=1-|y|,
两边平方,可得x2+y2=1+y2-2|y|,
即有x2=1-2|y|,
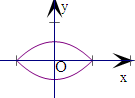
作出曲线W的图形,如右:
则由图象可得,O与点(-1,0)或(1,0)的距离最大,且为1;
O与点(0,
)或(0,-
)的距离最小,且为
.
故曲线W上的点到原点距离的取值范围是[
,1].
故选A.
 解:
解:| x2+y2 |
| x2+y2 |
两边平方,可得x2+y2=1+y2-2|y|,
即有x2=1-2|y|,
作出曲线W的图形,如右:
则由图象可得,O与点(-1,0)或(1,0)的距离最大,且为1;
O与点(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故曲线W上的点到原点距离的取值范围是[
| 1 |
| 2 |
故选A.
点评:本题考查曲线方程的化简,考查两点的距离公式的运用,考查数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
已知2sinx=a-1,则a的取值范围( )
| A、-1<a<3 |
| B、-1≤a≤3 |
| C、0<a<2 |
| D、0≤a≤2 |
与椭圆
+
=1共焦点,且与双曲线
-y2=1有相同渐近线的双曲线方程是( )
| x2 |
| 64 |
| y2 |
| 100 |
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将双曲线x2-y2=2绕原点逆时针旋转45°后可得到双曲线y=
,据此类推可求得双曲线y=
的焦距为( )
| 1 |
| x |
| 3 |
| x-1 |
A、2
| ||
B、2
| ||
| C、4 | ||
D、4
|
用二分法求函数f(x)=3x-x-4的一个零点,其参考数据如下:
据此数据,可得f(x)的一个零点的近似值(精确到0.01)为( )
| f(1.6)=0.200 | f(1.5875)=0.133 | f(1.5750)=0.067 |
| f(1.5625)=0.003 | f(1.5562)=-0.029 | f(1.550)=-0.060 |
| A、1.58 | B、1.57 |
| C、1.56 | D、1.55 |
如图,若在矩形OABC中随机一粒豆子,则豆子落在图中阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|