题目内容
4．计算：$\sum_{i=1}^{n}$[2（i-1）n+3]=$\frac{（-6+2i）}{5}[1-（i-1）^{n}]+3n$．分析 利用数列的分组求和，然后再由等比数列的前n项和得答案．
解答 解：$\sum_{i=1}^{n}$[2（i-1）2+3]=2[（i-1）+（i-1）2+（i-1）3+…+（i-1）n]+3n
=$2•\frac{（i-1）[1-（i-1）^{n}]}{1-（i-1）}+3n$=$2•\frac{（i-1）（2+i）[1-（i-1）^{n}]}{（2-i）（2+i）}+3n$
=$\frac{（-6+2i）}{5}[1-（i-1）^{n}]+3n$．
故答案为：$\frac{（-6+2i）}{5}[1-（i-1）^{n}]+3n$．
点评 本题考查复数代数形式的混合运算，考查了等比数列前n项和在复数中的应用，是中档题．
练习册系列答案
相关题目
一半径为4m的水轮，如图所示水轮圆心O距离水面2m，己知水轮每分钟转动4圈，如果当水轮上P点从水中浮现时（图中P0）点开始计算时间．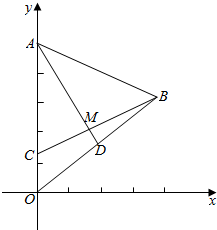
如图所示，已知△AOB中，A（0，5），O（0，0），B（4，3），$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$，$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$，AD与BC相交于点M，求点M的坐标．
12．在正项等比数列{an}中，若1og2（a1a2a3…a9）=18，且a2，a4是方程x2+mx+4=0的两根，则数列{an}的通项公式为（ ）
| A． | 2${\;}^{-\frac{n-3}{2}}$ | B． | 2${\;}^{\frac{n-3}{2}}$ | C． | 2${\;}^{\frac{n-1}{2}}$ | D． | 2${\;}^{\frac{n}{2}}$ |