题目内容
7．已知锐角△ABC中，角A、B、C所对边的角分别为a，b，c且$\overrightarrow{m}$=（a2+c2-b2，ac），$\overrightarrow{n}$=（tanB，-$\sqrt{3}$），$\overrightarrow{m}$$⊥\overrightarrow{n}$．（1）求角B的大小；
（2）若b=2，①求ac的最大值；②求a+c的取值范围．
分析 （1）根据向量的数量积运算，以及余弦定理和同角的三角函数的关系即可求出，
（2）根据余弦定理b2=a2+c2-2accosB以及基本不等式即可求出．
解答 解：（1）$\overrightarrow{m}$=（a2+c2-b2，ac），$\overrightarrow{n}$=（tanB，-$\sqrt{3}$），$\overrightarrow{m}$$⊥\overrightarrow{n}$，
∴$\overrightarrow{m}$•$\overrightarrow{n}$=（a2+c2-b2）tanB-3ac=0，
∴tanBcosB=$\frac{\sqrt{3}}{2}$，
∴sinB=$\frac{\sqrt{3}}{2}$，
∴B=$\frac{π}{3}$，
（2）由余弦定理，得b2=a2+c2-2accosB，即4=a2+c2-2ac×$\frac{1}{2}$，
∴ac+4=a2+c2≥2ac，即ac≤4，当且仅当a=c=2时取等号，
则ac的最大值为4，
∴（a+c）2=a2+c2+2ac=4+3ac≤16，又a+c＞b=2，
则a+c的取值范围是（2，4]．
点评 本题考查了向量的坐标运算以及向量的数量积以及余弦定理和基本不等式，属于中档题．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
17．
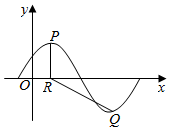如图所示为f（x）=Asin（$\frac{π}{6}$x+φ）（A＞0，0＜φ＜$\frac{π}{2}$）的部分图象，P，Q分别为f（x）图象的最高点和最低点，点P坐标为（2，A），PR⊥x轴于R，若∠PRQ=$\frac{2π}{3}$．则A及φ的值分别是（ ）
如图所示为f（x）=Asin（$\frac{π}{6}$x+φ）（A＞0，0＜φ＜$\frac{π}{2}$）的部分图象，P，Q分别为f（x）图象的最高点和最低点，点P坐标为（2，A），PR⊥x轴于R，若∠PRQ=$\frac{2π}{3}$．则A及φ的值分别是（ ）| A． | $\sqrt{3}$，$\frac{π}{6}$ | B． | $\sqrt{3}$，$\frac{π}{3}$ | C． | 2$\sqrt{3}$，$\frac{π}{6}$ | D． | 2$\sqrt{3}$，$\frac{π}{3}$ |
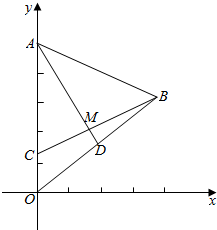如图所示，已知△AOB中，A（0，5），O（0，0），B（4，3），$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$，$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$，AD与BC相交于点M，求点M的坐标．
12．在正项等比数列{an}中，若1og2（a1a2a3…a9）=18，且a2，a4是方程x2+mx+4=0的两根，则数列{an}的通项公式为（ ）
| A． | 2${\;}^{-\frac{n-3}{2}}$ | B． | 2${\;}^{\frac{n-3}{2}}$ | C． | 2${\;}^{\frac{n-1}{2}}$ | D． | 2${\;}^{\frac{n}{2}}$ |