题目内容
8．函数f（x）=$\frac{1}{x-lnx}$的图象大致是（ ）| A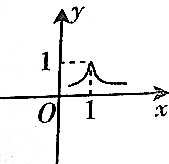． |  | B． |  | ||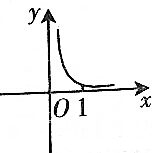
| C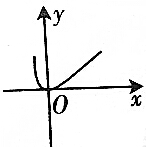． |  | D． |  |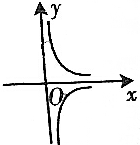
分析 求函数的导数，判断函数的单调性，利用函数的取值范围以及函数的性质进行排除即可．
解答 解：当x＜0时，lnx无应用，排除C．
∵f（x）=$\frac{1}{x-lnx}$是函数，∴排除D，
设g（x）=x-lnx，则g′（x）=1-$\frac{1}{x}$=$\frac{x-1}{x}$，
当x＞1时，g′（x）＞0，此时g（x）单调递增，且g（x）＞1-ln1=1，则f（x）=$\frac{1}{x-lnx}$为减函数，且f（x）＞0，
当0＜x＜1时，g′（x）＜0，此时g（x）单调递减，且g（x）＞1-ln1=1，则f（x）=$\frac{1}{x-lnx}$为增函数，且f（x）＞0，
排除B，
故选：A．
点评 本题主要考查函数图象的识别和判断，根据函数的性质，利用排除法是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目