题目内容
19.某农业科研实验室,对春季昼夜温差大小与某蔬菜种子发芽多少之间的关系进行研究,分别记录了3月1日至3月6日的每天昼夜温差与实验室每天每100粒种子浸泡后的发芽数,得到如表数据:| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 | 3月6日 |
| 昼夜温差(℃) | 9 | 11 | 13 | 12 | 8 | 10 |
| 发芽数(粒) | 23 | 25 | 30 | 26 | 16 | 24 |
(2)从3月1日至3月6日这六天中,按照日期从前往后的顺序任选2天记录发芽的种子数分别为m,n,用(m,n)的形式列出所有基本事件,并求满足$\left\{\begin{array}{l}{25≤m≤30}\\{25≤n≤30}\end{array}\right.$的事件A的概率.
分析 (1)根据平均数即可求出,
(2)一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
解答 解:(1)这6天的平均发芽率为:$\frac{{\frac{23}{100}+\frac{25}{100}+\frac{30}{100}+\frac{26}{100}+\frac{16}{100}+\frac{24}{100}}}{6}×100%=24%$,
∴这6天的平均发芽率为 24%,
(2)(m,n)的取值情况有
$\begin{array}{l}(23,25),(23,30),(23,26),(23,16),(23,24),\\(25,30),(25,26),(25,16),(25,24),\\(30,26),(30,16),(30,24),\\(26,16),(26,24),\\(16,24),\end{array}$
事件数为15,
设$\left\{\begin{array}{l}25≤m≤30\\ 25≤n≤30\end{array}\right.$为事件A,则事件A包含的基本事件为(25,30),(25,26)(30,26),
∴所求概率$P=\frac{3}{15}=\frac{1}{5}$.
点评 本题考查了平均数,独立事件的概率计算,关键是列举,属于基础题.

练习册系列答案
相关题目
10.若(x-a)2($\frac{1}{x}$-1)4的展开式中常数项为15,则a的值为( )
| A. | 1 | B. | 8 | C. | -1或9 | D. | 1或-9 |
14.在平面直角坐标系中,若不等式组$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{ax-y+1≥0}\end{array}\right.$,(a为常数)表示的区域面积等于3,则a的值为( )
| A. | -5 | B. | -2 | C. | 2 | D. | 5 |
4.平面内满足约束条件$\left\{\begin{array}{l}{y≥1}\\{y≤2x-1}\\{x+y≤8}\end{array}\right.$的点(x,y)形成的区域为M,区域M关于直线2x+y=0的对称区域为M′,则区域M和区域M′内最近的两点的距离为( )
| A. | $\frac{3\sqrt{3}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | $\frac{5\sqrt{5}}{5}$ | D. | $\frac{6\sqrt{5}}{5}$ |
6.已知集合A={x|3x2-5x-2≥0},B={x|x≤$\frac{3}{2}$},则(∁RA)∩B=( )
| A. | [-$\frac{1}{3}$,$\frac{3}{2}$] | B. | (-$\frac{1}{3}$,$\frac{3}{2}$] | C. | (-2,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
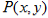 满足方程
满足方程 .
. 距离的最小值;
距离的最小值; ,若点
,若点 之间的最短距离为
之间的最短距离为 ,求满足条件的实数
,求满足条件的实数 的取值.
的取值.