题目内容
14．在平面直角坐标系中，若不等式组$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{ax-y+1≥0}\end{array}\right.$，（a为常数）表示的区域面积等于3，则a的值为（ ）| A． | -5 | B． | -2 | C． | 2 | D． | 5 |
分析 本题主要考查线性规划的基本知识，先画出约束条件的可行域，根据已知条件中，表示的平面区域的面积等于3，构造关于a的方程，解方程即可得到答案．
解答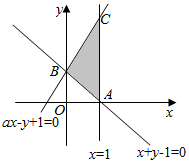 
解：不等式组$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{ax-y+1≥0}\end{array}\right.$，（a为常数）围成的区域如图所示．
∵由于x，y的不等式组所表示的平面区域的面积等于3，
∴$\frac{1}{2}$×|AC|×|xA-xB|=3，解得|AC|=6，
∴C的坐标为（1，6），
由于点C在直线ax-y+1=0上，
则a-6+1=0，解得a=5．
故选：D．
点评 平面区域的面积问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合有关面积公式求解．
练习册系列答案
相关题目
19．某农业科研实验室，对春季昼夜温差大小与某蔬菜种子发芽多少之间的关系进行研究，分别记录了3月1日至3月6日的每天昼夜温差与实验室每天每100粒种子浸泡后的发芽数，得到如表数据：
（1）求此种蔬菜种子在这6天的平均发芽率；
（2）从3月1日至3月6日这六天中，按照日期从前往后的顺序任选2天记录发芽的种子数分别为m，n，用（m，n）的形式列出所有基本事件，并求满足$\left\{\begin{array}{l}{25≤m≤30}\\{25≤n≤30}\end{array}\right.$的事件A的概率．
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 | 3月6日 |
| 昼夜温差（℃） | 9 | 11 | 13 | 12 | 8 | 10 |
| 发芽数（粒） | 23 | 25 | 30 | 26 | 16 | 24 |
（2）从3月1日至3月6日这六天中，按照日期从前往后的顺序任选2天记录发芽的种子数分别为m，n，用（m，n）的形式列出所有基本事件，并求满足$\left\{\begin{array}{l}{25≤m≤30}\\{25≤n≤30}\end{array}\right.$的事件A的概率．
6．已知集合A={x|y=$\sqrt{x-4}$}，B={x|-1≤2x-1≤0}，则∁RA∩B=（ ）
| A． | （4，+∞） | B． | [0，$\frac{1}{2}$] | C． | （$\frac{1}{2}$，4] | D． | （1，4） |