题目内容
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且当x∈[-1,1]时,f(x)=l-x2,函数g(x)=
,则函数h(x)=f(x)-g(x)在区问(-5,5)上的零点的个数是( )
|
| A、5 | B、6 | C、7 | D、8 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由题意可得,函数f(x)的周期为2,h(x)在区问(-5,5)上的零点的个数,就等于f(x)和g(x)的图象在区问(-5,5)上的交点的个数,数形结合求得f(x)和g(x)的图象在区问(-5,5)上的交点的个数.
解答:
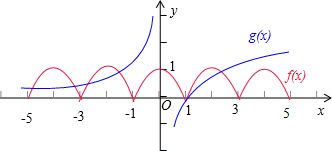 解:∵函数y=f(x)(x∈R)满足f(x+2)=f(x),故函数f(x)的周期为2,
解:∵函数y=f(x)(x∈R)满足f(x+2)=f(x),故函数f(x)的周期为2,
∵当x∈[-1,1]时,f(x)=l-x2,函数g(x)=
,函数h(x)=f(x)-g(x),
则h(x)在区问(-5,5)上的零点的个数,
就等于f(x)和g(x)的图象在区问(-5,5)上的交点的个数,如图所示:
显然,f(x)和g(x)的图象在区问(-5,5)上的交点的个数为6,
故选:B.
 解:∵函数y=f(x)(x∈R)满足f(x+2)=f(x),故函数f(x)的周期为2,
解:∵函数y=f(x)(x∈R)满足f(x+2)=f(x),故函数f(x)的周期为2,∵当x∈[-1,1]时,f(x)=l-x2,函数g(x)=
|
则h(x)在区问(-5,5)上的零点的个数,
就等于f(x)和g(x)的图象在区问(-5,5)上的交点的个数,如图所示:
显然,f(x)和g(x)的图象在区问(-5,5)上的交点的个数为6,
故选:B.
点评:本题主要考查方程根的存在性以及个数判断,体现了专户、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=(5a-1)x+2在R上是增函数,则a的取值范围是( )
| A、(-∞,+∞) | ||
B、(-∞,
| ||
C、(
| ||
| D、(5,+∞) |
已知x=2是函数f(x)=x3-3ax+2的极小值点,那么函数f(x)的极大值为( )
| A、15 | B、16 | C、17 | D、18 |
求值:(tan10°-
)sin40°=( )
| 3 |
| A、-1 | ||||
B、-
| ||||
C、-
| ||||
D、-
|
设集合A,B,则A⊆B是A∩B=A成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f(x)=2(m+1)x2+4mx+2m-1的一个零点在原点,则m的值为( )
| A、0 | ||
B、
| ||
C、-
| ||
| D、1 |
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x(1+x),则当x<0时,f(x)=( )
| A、x(1+x) |
| B、-x(1+x) |
| C、x(1-x) |
| D、-x(1-x) |