题目内容
4.定义域为{x|x>0}的函数f(x)满足f(xy)=f(x)+f(y)且f(8)=3,则$f({\sqrt{2}})$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{16}$ |
分析 由题意可得f(8)=f(2)+f(4)=f(2)+f(2)+f(2)=3f(2)=3(f($\sqrt{2}$)+f($\sqrt{2}$))=6f($\sqrt{2}$)=3,解得即可
解答 解:∵f(xy)=f(x)+f(y)且f(8)=3
∴f(8)=f(2)+f(4)=f(2)+f(2)+f(2)=3f(2)=3(f($\sqrt{2}$)+f($\sqrt{2}$))=6f($\sqrt{2}$)=3,
∴f($\sqrt{2}$)=$\frac{1}{2}$,
故选:A.
点评 本题考查了抽象函数的应用,关键是赋值,属于基础题.

练习册系列答案
相关题目
17.若实数a,b满足$\frac{1}{a}+\frac{4}{b}=\sqrt{ab}$,则ab的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
1.(x+y+2)6的展开式中x2y3的系数为( )
| A. | 360 | B. | 120 | C. | 60 | D. | 40 |
16.$(1+x){(1-\sqrt{x})^6}$展开式中x3项系数为( )
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
13.已知抛物线y2=2x上一点A到焦点F的距离与其到对称轴的距离之比为9:4,且|AF|>2,点A到原点的距离为( )
| A. | $\sqrt{41}$ | B. | 4$\sqrt{5}$ | C. | 4 | D. | 8 |
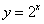 B.
B.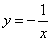
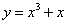 D.
D.
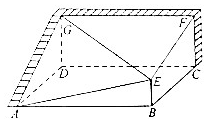 要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.
要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.