Question

14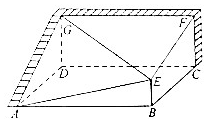．要利用现有的两面残墙，呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚（如图所示），所立柱子EB垂直于暖棚底面ABCD，其余四面计划用薄膜覆盖，已知底面ABCD是边长为2$\sqrt{6}$cm的正方形，且GD=2m，EB=1m．
（1）求二面角E-GF-C的大小（结果用反三角形式表示）；
（2）求直杆GE的长度；
（3）覆盖三角形AEG，至少需要多少面积的薄膜（结果精确到0.1m²）

Answer 1

分析 （1）由题意，二面角E-GF-C的平面角为∠EFC，即可求二面角E-GF-C的大小（结果用反三角形式表示）；
（2）利用勾股定理，求直杆GE的长度；
（3）求出三角形的三边，可得覆盖三角形AEG，至少需要多少面积的薄膜．

解答 解：（1）由题意，二面角E-GF-C的平面角为∠EFC，
∵底面ABCD是边长为2$\sqrt{6}$cm的正方形，∴BC=2$\sqrt{3}$，
∴tan∠EFC=2$\sqrt{3}$，
∴∠EFC=arctan2$\sqrt{3}$；
（2）GE=$\sqrt{12+12+1}$=5cm；
（3）△AEG中，GE=5，AE=$\sqrt{13}$，AG=4，
∴cos∠AGE=$\frac{25+16-13}{2•5•4}$=$\frac{7}{10}$，
∴sin∠AGE=$\frac{\sqrt{51}}{10}$，
∴S_△AEG=$\frac{1}{2}×5×4×\frac{\sqrt{51}}{10}$=$\sqrt{51}$≈7.1m²．

点评 本题考查二面角的平面角的计算，考查勾股定理、余弦定理的运用，属于中档题．