题目内容
函数f(x)=log
x+x-4的零点所在的区间是 .
| 1 |
| 2 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:判定出:f(
)=3+
-4<0,f(
)=4+
-4>0和f(6)=log
6+6-4=log
6+2<0,f(7)=log
7+7-3=log
7+4>0根据函数的零点的判定定理可求
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵f(
)=3+
-4<0,f(
)=4+
-4>0
∴函数f(x)=log
x+x-4的零点所在的区间是(
,
)
∵f(6)=log
6+6-4=log
6+2<0,
f(7)=log
7+7-3=log
7+4>0
∴函数f(x)=log
x+x-4的零点所在的区间是(6,7)
故答案为:(
,
)和(6,7)
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
∴函数f(x)=log
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 8 |
∵f(6)=log
| 1 |
| 2 |
| 1 |
| 2 |
f(7)=log
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)=log
| 1 |
| 2 |
故答案为:(
| 1 |
| 16 |
| 1 |
| 8 |
点评:本题主要考查了函数零点 定义及判定 的应用,属于基础试题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)=
,则下列函数的图象错误的是( )
|
A、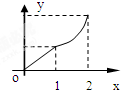 f(x-1)的图象 |
B、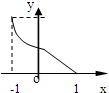 f(-x)的图象 |
C、 f(|x|)的图象 |
D、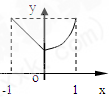 |f(x)|的图象 |