题目内容
在极坐标系内,已知曲线C1的方程为ρ2-2ρ(cosθ-2sinθ)+4=0,以极点为原点,极轴方向为x正半轴方向,利用相同单位长度建立平面直角坐标系,曲线C2的参数方程为
(t为参数).
(Ⅰ)求曲线C1的直角坐标方程以及曲线C2的普通方程;
(Ⅱ)设点P为曲线C2上的动点,过点P作曲线C1的切线,求这条切线长的最小值.
|
(Ⅰ)求曲线C1的直角坐标方程以及曲线C2的普通方程;
(Ⅱ)设点P为曲线C2上的动点,过点P作曲线C1的切线,求这条切线长的最小值.
考点:参数方程化成普通方程
专题:计算题,直线与圆,坐标系和参数方程
分析:(Ⅰ)运用x=ρcosθ,y=ρsinθ,x2+y2=ρ2,即可得到曲线C1的直角坐标方程,再由代入法,即可化简曲线C2的参数方程为普通方程;
(Ⅱ)可经过圆心(1,-2)作直线3x+4y-15=0的垂线,此时切线长最小.再由点到直线的距离公式和勾股定理,即可得到最小值.
(Ⅱ)可经过圆心(1,-2)作直线3x+4y-15=0的垂线,此时切线长最小.再由点到直线的距离公式和勾股定理,即可得到最小值.
解答:
解:(Ⅰ)对于曲线C1的方程为ρ2-2ρ(cosθ-2sinθ)+4=0,
可化为直角坐标方程x2+y2-2x+4y+4=0,
即圆(x-1)2+(y+2)2=1;
曲线C2的参数方程为
(t为参数),
可化为普通方程为:3x+4y-15=0.
(Ⅱ)可经过圆心(1,-2)作直线3x+4y-15=0的垂线,此时切线长最小.
则由点到直线的距离公式可得d=
=4,
则切线长为
=
.
故这条切线长的最小值为
.
可化为直角坐标方程x2+y2-2x+4y+4=0,
即圆(x-1)2+(y+2)2=1;
曲线C2的参数方程为
|
可化为普通方程为:3x+4y-15=0.
(Ⅱ)可经过圆心(1,-2)作直线3x+4y-15=0的垂线,此时切线长最小.
则由点到直线的距离公式可得d=
| |3×1+4×(-2)-15| | ||
|
则切线长为
| 16-1 |
| 15 |
故这条切线长的最小值为
| 15 |
点评:本题考查极坐标方程、参数方程和直角坐标方程、普通方程的互化,考查直线与圆相切的切线长问题,考查运算能力,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知函数y=sin(2x+φ)向左平移
个单位,所得函数图象关于y轴对称,则φ的最小正值为( )
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
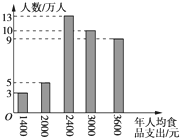 对“小康县”的经济评价标准:
对“小康县”的经济评价标准:①年人均收入不小于7000元;
②年人均食品支出不大于收入的35%.某县有40万人,调查数据如下:
| 年人均收入/元 | 0 | 2000 | 4000 | 6000 | 8000 | 10 000 | 12 000 | 16 000 |
| 人数/万人 | 6 | 3 | 5 | 5 | 6 | 7 | 5 | 3 |
| A、是小康县 |
| B、达到标准①,未达到标准②,不是小康县 |
| C、达到标准②,未达到标准①,不是小康县 |
| D、两个标准都未达到,不是小康县 |
若3a>1,则实数a的取值范围为( )
| A、a<0 | B、0<a<1 |
| C、a>0 | D、a>2 |