题目内容
8.已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0).双曲线C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为x$±\sqrt{3}$y=0,则C1与C2的离心率之积为( )| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
分析 由已知得a=$\sqrt{3}$k,b=k,k>0,从而得到椭圆C1的离心率e1=$\frac{\sqrt{3{k}^{2}-{k}^{2}}}{\sqrt{3}k}$=$\frac{\sqrt{2}}{\sqrt{3}}$,双曲线C2的离心率e2=$\frac{\sqrt{3{k}^{2}+{k}^{2}}}{\sqrt{3}k}$=$\frac{2}{\sqrt{3}}$,由此能求出C1与C2的离心率之积.
解答 解:∵椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0),双曲线C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为x$±\sqrt{3}$y=0,
∴a=$\sqrt{3}$k,b=k,k>0,
∴椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)的离心率e1=$\frac{\sqrt{3{k}^{2}-{k}^{2}}}{\sqrt{3}k}$=$\frac{\sqrt{2}}{\sqrt{3}}$,
双曲线C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率e2=$\frac{\sqrt{3{k}^{2}+{k}^{2}}}{\sqrt{3}k}$=$\frac{2}{\sqrt{3}}$,
∴C1与C2的离心率之积e1e2=$\frac{\sqrt{2}}{\sqrt{3}}×\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{2}}{3}$.
故选:D.
点评 本题考查双曲线的离心率和椭圆的离心率之积的求法,是中档题,解题时要认真审题,注意椭圆和双曲线的简章性质的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{13}$ | B. | 6 | C. | 2$\sqrt{14}$ | D. | 2$\sqrt{5}$ |
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
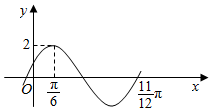 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.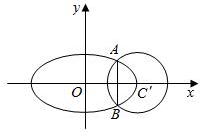 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,椭圆C与圆C′:(x-2)2+y2=1有且仅有A,B两个交点,且交点都在圆C′的左方,相交所得的弦AB长为$\frac{2\sqrt{5}}{3}$
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,椭圆C与圆C′:(x-2)2+y2=1有且仅有A,B两个交点,且交点都在圆C′的左方,相交所得的弦AB长为$\frac{2\sqrt{5}}{3}$