题目内容
7.若cos(π-θ)=$\frac{1}{3}$,且θ为第二象限角,则sin($\frac{3π}{2}$-θ)=$\frac{1}{3}$.分析 由条件利用诱导公式求得cosθ的值,从而求得sin($\frac{3π}{2}$-θ)的值.
解答 解:∵cos(π-θ)=-cosθ=$\frac{1}{3}$,∴cosθ=-$\frac{1}{3}$.
∵θ为第二象限角,∴sinθ=$\sqrt{{1-cos}^{2}θ}$=$\frac{2\sqrt{2}}{3}$,
则sin($\frac{3π}{2}$-θ)=-cosθ=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题主要考查诱导公式的应用,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
17.已知函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x=$\frac{2π}{3}$时,函数f(x)取得最小值,则下列结论正确的是( )
| A. | f(1)<f(-1)<f(0) | B. | f(0)<f(1)<f(-1) | C. | f(-1)<f(0)<f(1) | D. | f(1)<f(0)<f(-1) |
18.在平面直角坐标系xOy中,P是由不等式组$\left\{\begin{array}{l}x≥0\\ x-y-4≤0\\ x+y-4≤0\end{array}\right.$所确定的平面区域内的动点,Q是圆x2+y2-8x-8y+30=0上的动点,则|PQ|的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{2}-1$ |
20.若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1与$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率分别为e1,e2,且e1+e2=$\sqrt{3}$,则e1e2=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
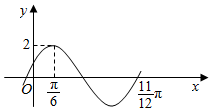 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.