题目内容
直线l:
(t为参数)与圆C:
(θ为参数)相交所得的弦长的取值范围是 .
|
|
考点:参数方程化成普通方程
专题:直线与圆,坐标系和参数方程
分析:把直线与圆的参数方程化为普通方程,画出图形,结合图形,求出直线被圆截得的弦长的最大值与最小值即可.
解答:
解:直线l:
(t为参数),
化为普通方程是
=
,
即y=tanα•x+1;
圆C的参数方程
(θ为参数),
化为普通方程是(x-2)2+(y-1)2=64;
画出图形,如图所示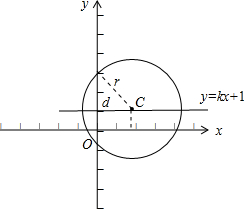 ;
;
∵直线过定点(0,1),
∴直线被圆截得的弦长的最大值是2r=16,
最小值是2
=2×
=2×
=4
∴弦长的取值范围是[4
,16].
故答案为:[4
,16].
|
化为普通方程是
| y-1 |
| x |
| sinα |
| cosα |
即y=tanα•x+1;
圆C的参数方程
|
化为普通方程是(x-2)2+(y-1)2=64;
画出图形,如图所示
 ;
;∵直线过定点(0,1),
∴直线被圆截得的弦长的最大值是2r=16,
最小值是2
| r2-d2 |
| 82-22 |
| 60 |
| 15 |
∴弦长的取值范围是[4
| 15 |
故答案为:[4
| 15 |
点评:本题考查了直线与圆的参数方程的应用问题,解题时先把参数方程化为普通方程,再画出图形,数形结合,容易解答本题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在空间中有一棱长为a的正四面体,其俯视图的面积的最大值为( )
| A、a2 | ||||
B、
| ||||
C、
| ||||
D、
|
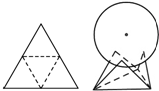 用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为
用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为