题目内容
已知3sin2α+2sin2β=1,3(sinα+cosα)2-2(sinβ+cosβ)2=1,则cos2(α+β)= .
考点:二倍角的余弦,两角和与差的余弦函数
专题:综合题,三角函数的求值
分析:利用3sin2α+2sin2β=1,可得3cos2α+2cos2β=3,利用3(sinα+cosα)2-2(sinβ+cosβ)2=1,可得3sin2α-2sin2β=0,从而可求得cos 2(α+β).
解答:
解:∵3sin2α+2sin2β=1,
∴3cos2α+2cos2β=3,①
又3sin2α+2sin2β=1,
∵3(sinα+cosα)2-2(sinβ+cosβ)2=1,
∴3(1+sin2α)-2(1+sin2β)=1,
∴3sin2α-2sin2β=0,②
①2+②2:13-12(cos2αcos2β-sin2αsin2β)=9
∴cos 2(α+β)=
.
故答案为:
.
∴3cos2α+2cos2β=3,①
又3sin2α+2sin2β=1,
∵3(sinα+cosα)2-2(sinβ+cosβ)2=1,
∴3(1+sin2α)-2(1+sin2β)=1,
∴3sin2α-2sin2β=0,②
①2+②2:13-12(cos2αcos2β-sin2αsin2β)=9
∴cos 2(α+β)=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查两角和与差的余弦函数,考查三角函数的化简求值,考查转化思想与综合运算能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
将函数h(x)=2sin(2x+
)的图象向右平移
个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象与函数h(x)的图象( )
| π |
| 4 |
| π |
| 4 |
| A、关于直线x=0对称 |
| B、关于直线x=1对称 |
| C、关于点(1,0)对称 |
| D、关于点(0,1)对称 |
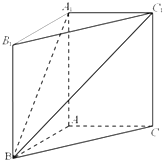 如图,在直三棱柱ABC-A1B1C1中,AC=AB=
如图,在直三棱柱ABC-A1B1C1中,AC=AB=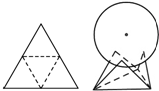 用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为
用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为