题目内容

（Ⅰ）已知函数：f（x）=2n-1（xn+a）-（x+a）n，（x∈[0，+∞），n∈N*）求函数f（x）的最小值；
（Ⅱ）证明：
a n+b n
2
≥（
a+b
2
）n（a＞0，b＞0，n∈N*）；
（Ⅲ）定理：若a1，a2，a3，ak均为正数，则有
a
n
1
+a
n
2
+a
n
3
+…
+a
n
k
k
≥（
a1+a2+a3+…ak
k
）n成立（其中k≥2，k∈N*，k为常数．请你构造一个函数g（x），证明：当a1，a2，a3，…ak，ak+1均为正数时，
a
n
1
+a
n
2
+a
n
3
+
…a
n
k+1
k+1
≥（
a1+a2+a3+…ak+1
k+1
）n．
考点：综合法与分析法(选修）,不等式的证明
专题：证明题,不等式
分析：（Ⅰ）求出函数的导数，求出极值点，判断函数的单调性，然后求出函数的最小值．
（Ⅱ）利用（Ⅰ）的结果，化简证明即可．
（Ⅲ）利用分析法，通过构造函数，利用函数的导数判断函数的单调性，通过函数的单调性证明不等式即可．
解答： 解：（Ⅰ）令f'（x）=2n-1nxn-1-n（a+x）n-1=0
得（2x）n-1=（a+x）n-1，∴2x=a+x，∴x=a---------------（2分）
当0≤x≤a时，∴2x＜a+x，∴f'（x）≤0，故f（x）在[0，a]上递减．
当x＞a，f'（x）＞0，故f（x）在（a，+∞）上递增．
∴，当x=a时，f（x）的最小值为f（a）=0---------------（4分）
（Ⅱ）由b＞0，有f（x）≥f（a）=0，即f（b）=2n-1（an+bn）-（a+b）n≥0
故　
an+bn
2
≥(
a+b
2
)n(a＞0，b＞0，n∈N*)．--------（5分）
（Ⅲ）证明：要证：
a
n
1
+
a
n
2
+
a
n
3
+…+
a
n
k+1
k+1
≥(
a1+a2+a3+…+ak+1
k+1
)n
只要证：(k+1)n-1(
a
n
1
+
a
n
2
+
a
n
3
+…+
a
n
k+1
)≥(a1+a2+a3+…+ak+1)n
设g(x)=(k+1)n-1(
a
n
1
+
a
n
2
+
a
n
3
+…+xn)-(a1+a2+a3+…+x)n-------------（7分）
则g′(x)=(k+1)n-1•nxn-1-n(a1+a2+a3+…+x)n-1
令g'（x）=0得x=
a1+a2+a3+…+ak
k
---------------（8分）
当0≤x≤
a1+a2+a3+…+ak
k
时，g′(x)=(k+1)n-1•nxn-1-n(a1+a2+a3+…+x)n-1
≤n(a1+a2+a3+…+x)n-1-n(a1+a2+a3+…+x)n-1=0
故g（x）在[0，
a1+a2+a3+…+ak
k
]上递减，
类似地可证g（x）在[
a1+a2+a3+…+ak
k
，+∞)递增
∴当x=
a1+a2+a3+…+ak
k
时，g（x）的最小值为g(
a1+a2+a3+…+ak
k
)------------（10分）
而g(
a1+a2+a3+…+ak
k
)
=(k+1)n-1(
a
n
1
+
a
n
2
+…+
a
n
k
+(
a1+a2+a3+…+ak
k
)n)-(a1+a2+…+ak+
a1+a2+a3+…+ak
k
)n
=
(k+1)n-1
kn
[kn(
a
n
1
+
a
n
2
+…+
a
n
k
+(a1+a2+a3+…+ak)n)-(k+1)(a1+a2+…+ak)n]
=
(k+1)n-1
kn
[kn(
a
n
1
+
a
n
2
+…+
a
n
k
)-k(a1+a2+…+ak)n]
=
(k+1)n-1
kn-1
[kn-1(
a
n
1
+
a
n
2
+…+
a
n
k
)-(a1+a2+…+ak)n]
由定理知：kn-1(
a
n
1
+
a
n
2
+…+
a
n
k
)-(a1+a2+…+ak)n≥0，
故g(
a1+a2+a3+…+ak
k
)≥0
∵ak+1∈[0，+∞），
∴g(ak+1)≥g(
a1+a2+a3+…+ak
k
)≥0
故(k+1)n-1(
a
n
1
+
a
n
2
+
a
n
3
+…+
a
n
k+1
)≥(a1+a2+a3+…+ak+1)n
即：
a
n
1
+
a
n
2
+
a
n
3
+…+
a
n
k+1
k+1
≥(
a1+a2+a3+…+ak+1
k+1
)n---------------（14分）
点评：本题考查函数的单调性，分析法构造法以及函数的导数的综合应用，难度比较大．
练习册系列答案
相关题目
计算：
(1+i)2006
(-
1
2
+
3
2
i)6
+
21003
i2015
．
已知椭圆的中心在原点，焦点在坐标轴上，与过点P（1，2）且斜率为-2的直线l相交所得的弦恰好被点P平分，求椭圆的离心率．
一个正方形的中心到各顶点的连线，能构成多少个向量？试写出所构成的全部向量；若正方形的边长为1，求所有向量的模．
如图，四棱锥S-ABCD中，SD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=SD=2，E为棱SB上任一点．
（Ⅰ）求证：无论E点取在何处恒有BC⊥DE；
（Ⅱ）设
SE
=λ
EB
，当平面EDC⊥平面SBC时，求λ的值；
（Ⅲ）在（Ⅱ）的条件下求二面角A-DE-C的大小．
已知圆C：x2+（y-1）2=5，直线l：mx-y+1-m=0，求直线l截圆所得的弦最长及最短时的方程．
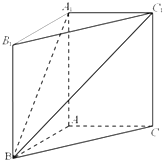如图，在直三棱柱ABC-A1B1C1中，AC=AB=
2
，∠BAC=90°，且异面直线A1B与B1C1所成的角等于60°．
（Ⅰ）求棱柱的高；
（Ⅱ）求B1C1与平面A1BC1所成的角的大小．
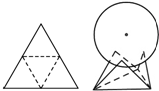用一个边长为4的正三角形硬纸，沿各边中点连线垂直折起三个小三角形，做成一个蛋托，半径为1的鸡蛋（视为球体）放在其上（如图），则鸡蛋中心（球心）与蛋托底面的距离为
 
．
已知圆锥底面圆的周长为4π，侧棱与底面所成角的大小为arctan2，则该圆锥的体积是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网