题目内容

已知|
a
|=4，|
b
|=3，（2
a
-3
b
）•（2
a
+
b
）=61，
（1）求
a
与
b
夹角θ；  
（2）求|
a
-2
b
|．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由已知条件，利用向量的运算法则，求出cos＜
a
，
b
＞的值，由此能求出
a
与的
b
夹角θ．
（2）由已知条件，利用公式|
a
-2
b
|=
(
a
-2
b
)2
，能求出结果．
解答： 解：（1）∵|
a
|=4，|
b
|=3，（2
a
-3
b
）•（2
a
+
b
）=61，
∴（2
a
-3
b
）•（2
a
+
b
）
=4
a
2-4
a
•
b
-3
b
2
=4×42-4×4×3×cos＜
a
，
b
＞-3×32
=61，
解得cos＜
a
，
b
＞=-
1
2
，
∴
a
与的
b
夹角θ=
2π
3
．
（2）|
a
-2
b
|=
(
a
-2
b
)2

=
a
2-4
a
•
b
+4
b
2

=
42-4×4×3×cos
2π
3
+4×32

=2
19
．
点评：本题考查平面向量的夹角和模的求法，是中档题，要熟练掌握平面向量的运算法则．
练习册系列答案
相关题目
若
a
=（a1，a2，a3），
b
=（b1，b2，b3），则
a1
b1
=
a2
b2
=
a3
b3
是
a
∥
b
的（　　）
A、既不充分也不必要条件
B、必要不充分条件
C、充要条件
D、充分不必要条件
已知函数f（x）=x2+bx+c，其中0≤b≤4，0≤c≤4，记事件A为“函数f（x）满足条件：
(f(2))≤12
f(-1)≤1
”，则事件A发生的概率为（　　）
A、
4
9
B、
1
3
C、
1
2
D、
1
9
在△ABC中，A=
π
3
，C=
π
6
，b=2，则此三角形的最小边长是（　　）
A、1
B、2
3
-2
C、
3
-1
D、
3
2
设关于x的函数y=2cos2x-2acosx-（2a+1）的最小值为f（a），试确定满足f(a)=
1
2
的a的值，并对此时的a值求y的最大值及对应x的集合．
（1）已知方程sin（α-3π）=2cos（α-4π），求
sin(π-α)+5cos(2π-α)
2sin(
3π
2
-α)-sin(-α)
的值．
（2）已知tanα，
1
tanα
是关于x的方程，x2-kx+k2-3=0的两个实根，且3π＜α＜
7
2
π，求cosα+sinα的值．
已知2sin2α-sinαcosα+5cos2α=3，求：
（1）tanα
（2）sinα•cosα
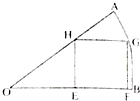如图所示，扇形OAB中，∠AOB=
π
3
，半径r=2cm，内接矩形EFGH，它的一条边EF在OB上，则矩形面积的最大值为
 
．
已知集合A={x|y=
x+1
}，B={x|
x-1
x+1
≤0}，则A∩B=（　　）
A、（-1，1]
B、[-1，1]
C、[1，+∞）
D、[0，1]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网