Question

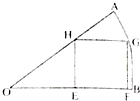如图所示，扇形OAB中，∠AOB=

π

3

，半径r=2cm，内接矩形EFGH，它的一条边EF在OB上，则矩形面积的最大值为

 

．

Answer 1

考点：已知三角函数模型的应用问题

专题：计算题,三角函数的求值

分析：计算PN、MN的长，从而可得面积表达式，再利用辅助角公式化简函数，利用角的范围，即可求得面积的最大值．

解答： 解：，扇形OAB中，∠AOB=

π

3

，半径r=2cm，内接矩形EFGH，它的一条边EF在OB上，
设∠GOB=θ，θ∈（0，

π

3

）
，FG=HE=2sinθ，OF=2cosθ，OE=

2sinθ

tan π 3

=

2 3

3

sinθ，
矩形面积：S=HE•EF=2sinθ（OF-OE）=2sinθ（2cosθ-

2 3

3

sinθ）
=2sin2θ-

4 3

3

sin2θ
=2sin2θ-

2 3

3

(1-cos2θ)
=2sin2θ+2

3

3

cos2θ-

2 3

3

=

4 3

3

sin(2x+

π

6

)-

2 3

3

∵θ∈（0，

π

3

）
∴2θ+

π

6

∈（

π

6

，

5π

6

）
∴sin（2θ+

π

6

）∈（

1

2

，1]
∴2θ+

π

6

=

π

2

，即θ=

π

6

时，S的最大值为

2 3

3

．

点评：本题考查三角函数模型的应用问题，是中档题．解题时要认真审题，注意垂径定理、勾股定理、直角三角形的性质的灵活运用，合理地进行等价转化．