题目内容
9．已知向量$\overrightarrow{a}$=（-4，x），$\overrightarrow{b}$=（5，2），若$\overrightarrow{a}$⊥$\overrightarrow{b}$．则x=10．分析 令$\overrightarrow{a}•\overrightarrow{b}$=0解出．
解答 解：∵$\overrightarrow{a}$⊥$\overrightarrow{b}$，∴$\overrightarrow{a}$•$\overrightarrow{b}$=-20+2x=0，∴x=10．
故答案为10．
点评 本题考查了向量垂直与数量积的关系，属于基础题．
练习册系列答案
相关题目
17．若|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{π}{3}$，则|2$\overrightarrow{a}$$-\overrightarrow{b}$|=（ ）
| A． | 2 | B． | 2$\sqrt{3}$ | C． | 0 | D． | $\sqrt{2}$ |
14．已知R上的可导偶函数f（x）满足f（x+2）=f（x-2），又f′（1）=5，则f′（15）的值为（ ）
| A． | 5 | B． | -5 | C． | 0 | D． | ±5 |
1．函数f（x）=x+$\frac{{a}^{2}}{x}$（a＞0）的减区间为（ ）
| A． | （-a，a） | B． | （-a，0），（0，a） | C． | （-a，0）∪（0，a） | D． | 以上皆非 |
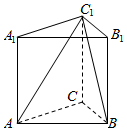如图，三棱柱的侧棱长为2，底面是边长为2的正三角形，AA1⊥面A1B1C1，正视图是边长为2正方形．