题目内容
方程sinπx=-
x的解的个数是( )
| 1 |
| 4 |
| A、5 | B、6 | C、7 | D、8 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:在同一个坐标系中作出y=sinπx 和y=-
x的图象,根据y=sinπx 和y=-
x的图象有7个交点,可得方程sinπx=-
x的解的个数是7.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:在同一个坐标系中作出y=sinπx和y=-
x的图象,如图所示:

由于y=sinπx和y=-
x的图象在[-4,4]上有7个交点,
而当x<-4,或 x>4时,两个曲线不会有交点,
方程sinπx=-
x的解的个数是7,
故选:C
| 1 |
| 4 |

由于y=sinπx和y=-
| 1 |
| 4 |
而当x<-4,或 x>4时,两个曲线不会有交点,
方程sinπx=-
| 1 |
| 4 |
故选:C
点评:本题考查正弦函数的图象特征,利用两曲线交点的个数判断方程的解的个数,体现了数形结合的数学思想,画出图形,是解题的关键

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
函数f(x)的定义域为[0,2],则函数f(x2)的定义域是 ( )
| A、[-2,2] | ||||
B、[-
| ||||
| C、[0,2] | ||||
| D、[0,4] |
方程sinx=
x2的正实根个数为( )
| 1 |
| 100 |
| A、2个 | B、3个 | C、4个 | D、无数个 |
定义在R上的偶函数在[0,7]上是减函数,则f(x)( )
| A、在[-7,0]上是增函数 |
| B、在[-7,0]上是减函数 |
| C、在[7,+∞)上是减函数 |
| D、在[-7,7]是增函数 |
方程x2=cosx的实根的个数是( )
| A、0 | B、1 | C、2 | D、3 |
| ∫ | 2π 0 |
| A、0 | B、2 | C、-2 | D、4 |
已知函数f(x)=1-2x,g(x)=x2-4x+3,若关于x的方程f(x)=g(a)总有解,则实数a的取值范围为( )
A、[2-
| ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
设全集U=R,A={x|-3<x<0},B={x|x<-1},则图中阴影部分表示的集合为( )
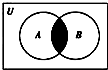

| A、(-3,-1) |
| B、(-1,0) |
| C、[-1,0) |
| D、(-∞,-1) |