题目内容
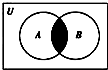
设全集U=R，A={x|-3＜x＜0}，B={x|x＜-1}，则图中阴影部分表示的集合为（ ）
| A、（-3，-1） |
| B、（-1，0） |
| C、[-1，0） |
| D、（-∞，-1） |
考点：Venn图表达集合的关系及运算
专题：集合
分析：分析可得，图中阴影部分表示的为集合A、B的公共部分，即A∩B，由集合A、B计算A∩B即可得答案．
解答：
解：根据题意，分析可得，图中阴影部分表示的为集合A、B的公共部分，即A∩B，
又由A={x|-3＜x＜0}，B={x|x＜-1}，得A∩B={x|-3＜x＜-1}=（-3，-1），
故选：A
又由A={x|-3＜x＜0}，B={x|x＜-1}，得A∩B={x|-3＜x＜-1}=（-3，-1），
故选：A
点评：本题考查Venn图表示集合，关键是分析阴影部分表示的集合，注意答案必须为集合或区间的形式．
练习册系列答案
相关题目
方程sinπx=-
x的解的个数是（ ）
| 1 |
| 4 |
| A、5 | B、6 | C、7 | D、8 |
若集合A={α|α是第一象限角}，B={β|β是锐角}，C={γ|γ＜90°}，则（ ）
| A、A⊆C | B、A∩C=B |
| C、A∪B=A | D、以上都不对 |
已知二项式（1-2x）n展开式中，第5项的二项式系数最大，满足要求的正整数n的集合为M，则集合M所有非空子集的元素之和为（ ）
| A、96 | B、34 | C、30 | D、8 |
定义域为R的函数y=f（x）的值域为[a，b]，则函数y=f（x-3a）的值域为（ ）
| A、[2a，a+b] |
| B、[0，b-a] |
| C、[a，b] |
| D、[-a，a+b] |
以M（-4，3）为圆心的圆与直线2x+y-5=0相离，那么圆M的半径r的取值范围是（ ）
| A、0＜r＜2 | ||
B、0＜r＜
| ||
C、0＜r＜2
| ||
| D、0＜r＜10 |
已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（ ）
A、f（x）=2sin（
| ||||
B、f（x）=
| ||||
C、f（x）=2cos（
| ||||
D、f（x）=2sin（4x+
|
已知直线kx-y+k+1=0（k∈R）上存在点（x，y）满足
，则实数k的取值范围为（ ）
|
A、[-
| ||||
B、（-∞，-
| ||||
C、[-1，
| ||||
D、[-
|