题目内容
14.设α,β,γ为平面,m,n,l为直线,则m⊥β的一个充分条件是( )| A. | α⊥β,α∩β=l,m⊥l | B. | n⊥α,m⊥α,n⊥β | C. | α⊥γ,β⊥γ,m⊥α | D. | α⊥γ,α∩γ=m,β⊥γ |
分析 A.根据面面垂直的判定定理可知,缺少条件m?α,即可判断出正误;
B.根据线面垂直的判定与性质即可判断出正误;
C.α与β可能平行,也可能相交,则m与β不一定垂直,即可判断出正误;
D.利用线面垂直与平行的判定性质定理即可判断出正误.
解答 解:A.α⊥β,α∩β=l,m⊥l,根据面面垂直的判定定理可知,缺少条件m?α,故A不正确;
B.n⊥α,m⊥α,∴m∥n,又n⊥β,∴m⊥β,因此B正确;
C.α⊥γ,β⊥γ,m⊥α,而α与β可能平行,也可能相交,则m与β不一定垂直,故C不正确;
D.α⊥γ,α∩γ=m,β⊥γ,则m可能与β平行,相交,故D不正确.
故选:B.
点评 本题考查了空间位置关系,考查了空间想象能力、推理能力,属于中档题.

练习册系列答案
相关题目
9.阅读如图的程序框图,运行相应的程序,输出的结果为( )
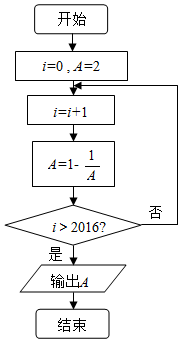

| A. | -2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2 |
6.“a≠1”是“a2≠1”的( )
| A. | 充分不必条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.
如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.