题目内容
16.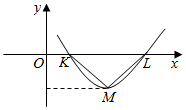 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}+\sqrt{6}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
分析 由条件利用等腰直角三角形求出A,由周期求出ω,由函数的奇偶性求出φ的值,可得f(x)的解析式,再利用两角差的余弦公式,求得f($\frac{1}{12}$)的值.
解答 解:由题意可得$\frac{1}{2}$•$\frac{2π}{ω}$=KL=1,∴ω=π,KM=$\frac{\sqrt{2}}{2}$=$\sqrt{{(\frac{1}{2})}^{2}{+A}^{2}}$,∴A=$\frac{1}{2}$,∴f(x)=$\frac{1}{2}$sin(πx+φ).
再结合f(x)为偶函数,以及所给的图象,可得φ=$\frac{π}{2}$,∴f(x)=$\frac{1}{2}$cos(πx).
则f($\frac{1}{12}$)=$\frac{1}{2}$cos($\frac{π}{12}$)=$\frac{1}{2}$•cos($\frac{π}{3}$-$\frac{π}{4}$)=$\frac{1}{2}$[cos$\frac{π}{3}$cos$\frac{π}{4}$+sin$\frac{π}{3}$sin$\frac{π}{4}$]=$\frac{1}{2}$•[$\frac{1}{2}•\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}•\frac{\sqrt{2}}{2}$]=$\frac{\sqrt{2}+\sqrt{6}}{8}$,
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由条件利用等腰直角三角形求出A,由周期求出ω,由函数的奇偶性求出φ的值,两角差的余弦公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若x、y满足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$,若z=x+2y的最大值是6,则z的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.已知集合A={1,2,3},B={x|x2<9},则A∩B=( )
| A. | {-2,-1,0,1,2,3} | B. | {-2,-1,0,1,2} | C. | {1,2,3} | D. | {1,2} |
11.集合A={x∈N|x2-2x-3<0},B={1,x2},若A∪B={0,1,2},则这样的实数x的个数为( )
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 3个 |
6.体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )
| A. | 12π | B. | $\frac{32}{3}$π | C. | 8π | D. | 4π |