题目内容
2．已知集合A={1，2，3}，B={x|x2＜9}，则A∩B=（ ）| A． | {-2，-1，0，1，2，3} | B． | {-2，-1，0，1，2} | C． | {1，2，3} | D． | {1，2} |
分析 先求出集合A和B，由此利用交集的定义能求出A∩B的值．
解答 解：∵集合A={1，2，3}，B={x|x2＜9}={x|-3＜x＜3}，
∴A∩B={1，2}．
故选：D．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
13．已知单位向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{5}$ | C． | $\sqrt{3}$ | D． | $\sqrt{7}$ |
10．
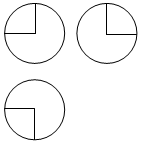如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是$\frac{28π}{3}$，则它的表面积是（ ）
如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是$\frac{28π}{3}$，则它的表面积是（ ）| A． | 17π | B． | 18π | C． | 20π | D． | 28π |
17．已知z=（m+3）+（m-1）i在复平面内对应的点在第四象限，则实数m的取值范围是（ ）
| A． | （-3，1） | B． | （-1，3） | C． | （1，+∞） | D． | （-∞，-3） |
14．从甲、乙等5名学生中随机选出2人，则甲被选中的概率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{8}{25}$ | D． | $\frac{9}{25}$ |
16．
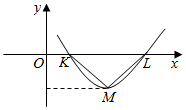设偶函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，△KLM为等腰直角三角形，∠KML=90°，KL=1，则f（$\frac{1}{12}$）的值为（ ）
设偶函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，△KLM为等腰直角三角形，∠KML=90°，KL=1，则f（$\frac{1}{12}$）的值为（ ）| A． | $\frac{\sqrt{6}-\sqrt{2}}{8}$ | B． | $\frac{\sqrt{2}+\sqrt{6}}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{\sqrt{3}}{4}$ |
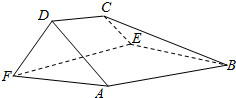如图，在以A，B，C，D，E，F为顶点的五面体中，面ABEF为正方形，AF=2FD，∠AFD=90°，且二面角D-AF-E与二面角C-BE-F都是60°．