题目内容
6.体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )| A. | 12π | B. | $\frac{32}{3}$π | C. | 8π | D. | 4π |
分析 先通过正方体的体积,求出正方体的棱长,然后求出球的半径,即可求出球的表面积.
解答 解:正方体体积为8,可知其边长为2,
正方体的体对角线为$\sqrt{4+4+4}$=2$\sqrt{3}$,
即为球的直径,所以半径为$\sqrt{3}$,
所以球的表面积为$4π•(\sqrt{3})^{2}$=12π.
故选:A.
点评 本题考查学生的空间想象能力,体积与面积的计算能力,是基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
16.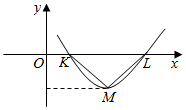 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}+\sqrt{6}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
11.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
(I)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(Ⅲ)求续保人本年度的平均保费估计值.
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(Ⅲ)求续保人本年度的平均保费估计值.
18.某三棱锥的三视图如图所示,则该三棱锥的体积为( )


| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
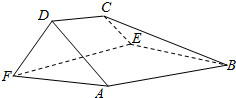 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.