题目内容
8.在平面直角坐标系xoOy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ=$\frac{π}{4}$(ρ∈R),曲线C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}$(θ为参数).(1)写出直线l与曲线C的直角坐标方程;
(2)过点M平行于直线l的直线与曲线C交于A、B两点,若|MA|•|MB|=3,求点M轨迹的直角坐标方程.
分析 (1)根据题意,由极坐标方程的定义可得直线l的方程,对于曲线C的参数方程,消去参数计算即可得答案;
(2)设点M(x0.y0)及过点M的直线为${L_1}:\left\{\begin{array}{l}x={x_0}+\frac{{\sqrt{2}}}{2}t\\ y={y_0}+\frac{{\sqrt{2}}}{2}t\end{array}\right.(t为参数)$,结合题意直线L1与曲线C相交可得:${t^2}+\sqrt{2}({{x_0}+{y_0}})t+{x_0}^2+{y_0}^2-1=0$,又由题意可得$|{{x_0}^2+{y_0}^2-1}|=3$,将其变形可得答案.
解答 解:(1)直线l的极坐标方程为θ=$\frac{π}{4}$,所以直线斜率为1,直线l:y=x;
曲线C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.(θ为参数)$,消去参数θ,
可得曲线C:x2+y2=1,
(2)设点M(x0.y0)及过点M的直线为${L_1}:\left\{\begin{array}{l}x={x_0}+\frac{{\sqrt{2}}}{2}t\\ y={y_0}+\frac{{\sqrt{2}}}{2}t\end{array}\right.(t为参数)$,
由直线L1与曲线C相交可得:${t^2}+\sqrt{2}({{x_0}+{y_0}})t+{x_0}^2+{y_0}^2-1=0$,
因为|MA|•|MB|=3
所以$|{{x_0}^2+{y_0}^2-1}|=3$,即:${x_0}^2+{y_0}^2=4$,
$\left\{\begin{array}{l}y=x+m\\{x^2}+{y^2}=1\end{array}\right.⇒2{x^2}+2mx+{m^2}-1=0$
由$△>0⇒-\sqrt{2}<m<\sqrt{2}$
故点M的轨迹的直角坐标方程为:x2+y2=4(夹在两直线$y=x±\sqrt{2}$之间的两段圆弧)
点评 本题考查极坐标以及参数方程的应用,涉及极坐标方程、参数方程与直角坐标系方程的转化,关键是掌握极坐标方程、参数方程的意义.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{8}{25}$ | D. | $\frac{9}{25}$ |
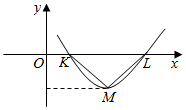 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}+\sqrt{6}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |

| A. | ②④③① | B. | ④②③① | C. | ③①②④ | D. | ④①②③ |

| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
 如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.
如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.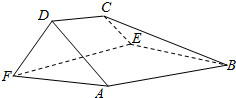 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.