题目内容
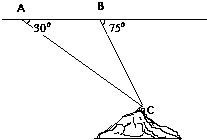如图，飞机的航线和山顶在同一铅垂面内，若飞机的高度为海拔18km，速度为1000km/h，飞行员先看到山顶的俯角为30°，经过1min后又看到山顶的俯角为75°，则山顶的海拔高度为（精确到0.1）（ ）| A、11.4 | B、6.6 |
| C、6.5 | D、5.6 |
考点：解三角形的实际应用
专题：应用题,解三角形
分析：根据题意求得∠ACB和AB的长，然后利用正弦定理求得BP，最后利用BP•sin75°求得问题的答案．
解答：
解：在△ABP中，∠BAC=30°，∠ACB=75°-30°=45°，AB=1000×
=
．
根据正弦定理，
=
，
∴BC=
．
BP•sin75°=
×sin（45°+30°）≈11.5．
所以，山顶P的海拔高度为h=18-11.4=6.5（千米）．
故选：C．
| 1 |
| 60 |
| 50 |
| 3 |
根据正弦定理，
| ||
| sin45° |
| BC |
| sin30° |
∴BC=
| 25 |
| 3 |
| 2 |
BP•sin75°=
| 25 |
| 3 |
| 2 |
所以，山顶P的海拔高度为h=18-11.4=6.5（千米）．
故选：C．
点评：本题主要考查了解三角形问题的应用．注意把实际问题与三角函数的知识相联系，建立相应的数学模型．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=
的定义域为（ ）
| x2-x-2 |
| A、{x|x≤-1或x≥2} |
| B、{x|x＜2} |
| C、R |
| D、{x|x≤-1且x≥2} |
已知f（x）=
的定义域为A，值域为B，则∁A（A∩B）=（ ）
| x2-x+2 |
A、[
| ||||
B、（-∞，-
| ||||
C、（-∞，
| ||||
| D、（-∞，-1） |