题目内容
函数f(x)=-x3+3x2在[-1,1]上的最大、小值分别为M和m,则
f(x)dx= .
| ∫ | M m |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:利用导数求出函数的最大值和最小值,然后利用函数的积分公式即可得到结论.
解答:
解:函数的导数为f′(x)=-3x2+6x,
由f′(x)=-3x2+6x=0得x=0或2,
∵x∈[-1,1],
∴f′(x)=-3x2+6x=0的根为x=0.
当x∈(-1,0)时f′(x)<0,此时函数单调递减,
当x∈(0,1)时f′(x)>0.此时函数单调递增,
∴x=0时,f(x)取极小值f(0)=0.
又f(-1)=4,f(1)=2
∴最大值M=4,最小值m=0,
∴
f(x)dx=
(-x3+3x2)dx=(-
x4+x3
=0,
故答案为:0
由f′(x)=-3x2+6x=0得x=0或2,
∵x∈[-1,1],
∴f′(x)=-3x2+6x=0的根为x=0.
当x∈(-1,0)时f′(x)<0,此时函数单调递减,
当x∈(0,1)时f′(x)>0.此时函数单调递增,
∴x=0时,f(x)取极小值f(0)=0.
又f(-1)=4,f(1)=2
∴最大值M=4,最小值m=0,
∴
| ∫ | M m |
| ∫ | 4 0 |
| 1 |
| 4 |
| )| | 4 0 |
故答案为:0
点评:本题主要考查积分的计算,利用导数求出函数的最值是解决本题的关键,要求熟练掌握函数的积分公式.

练习册系列答案
相关题目
设a=(
) log23,b=(
) log54,c=3ln3,则a,b,c的大小关系是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、c>a>b |
| B、c>b>a |
| C、a>b>c |
| D、a>c>b |
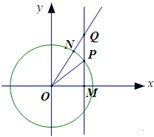 在直角坐标系xOy中,点p是单位圆上位于第一象限的动点,过p作x轴的垂线与射线y=xtanθ(x≥0,0<θ<
在直角坐标系xOy中,点p是单位圆上位于第一象限的动点,过p作x轴的垂线与射线y=xtanθ(x≥0,0<θ<