题目内容
设a=（
） log23，b=（
） log54，c=3ln3，则a，b，c的大小关系是（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| A、c＞a＞b |
| B、c＞b＞a |
| C、a＞b＞c |
| D、a＞c＞b |
考点：对数的运算性质,根式与分数指数幂的互化及其化简运算
专题：函数的性质及应用
分析：利用指数函数和对数函数的单调性即可得出．
解答：
解：a=（
） log23=3-log23，b=（
） log54=3-log54，c=3ln3，
又ln3＞1＞0＞-log54＞-1＞-log23，
∴3ln3＞3-log54＞3-log23，
∴c＞b＞a．
故选：B．
| 1 |
| 3 |
| 1 |
| 3 |
又ln3＞1＞0＞-log54＞-1＞-log23，
∴3ln3＞3-log54＞3-log23，
∴c＞b＞a．
故选：B．
点评：本题考查了指数函数和对数函数的单调性，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设函数f（x）的定义域为D，如果?x∈D，?y∈D，使得f（x）=-f（y）成立，则称函数f（x）为“Ω函数”．给出下列四个函数：
①y=sinx；
②y=2x；
③y=
；
④f（x）=lnx，
则其中“Ω函数”共有（ ）
①y=sinx；
②y=2x；
③y=
| 1 |
| x-1 |
④f（x）=lnx，
则其中“Ω函数”共有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
复数
（i为虚数单位）的虚部是（ ）
| 2 |
| 1+i |
| A、1 | B、-1 | C、-i | D、i |
一几何体的三视图如图，该几何体的顶点都在球O的球面上，球O的表面积是（ ）
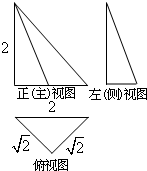
| A、2π | B、4π | C、8π | D、16π |
（tan80°-4cos10°）•
=（ ）
| 3-sin70° |
| 2-cos210° |
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
已知某几何体的三视图（单位：cm）如图所示，则该几何体的表面积是（ ）| A、1cm2 | ||||
| B、3cm2 | ||||
C、（2
| ||||
D、（
|
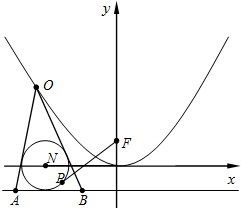已知圆N：（x+3）2+y2=1，抛物线C：y=mx2（m＞0）的焦点为（0，1）．