题目内容
7.已知圆C的圆心在x轴上,并且过点A(-1,1)和B(1,3)(Ⅰ)求圆C的方程;
(Ⅱ)若过点A的直线l被圆C截得的弦长为$4\sqrt{2}$,求直线l的方程.
分析 (Ⅰ)设圆心为M(a,0),由|MA|=|MB|求得a的值,可得圆心坐标以及半径的值,从而求得圆的方程.
(Ⅱ)求出圆心到直线的距离,即可求直线l的方程.
解答 解:(Ⅰ)∵圆C的圆心在x轴上,设圆心为M(a,0),由圆过点A(-1,1)和B(1,3),
由|MA|=|MB|可得 MA2=MB2,即(a+1)2+1=(a-1)2+9,求得a=2,
可得圆心为M( 2,0),半径为|MA|=$\sqrt{10}$,故圆的方程为 (x-2)2+y2=10,
(Ⅱ)直线l被圆C截得的弦长为$4\sqrt{2}$,∴圆心到直线的距离d=$\sqrt{10-8}$=$\sqrt{2}$.
设直线方程为y-1=k(x+1),即kx-y+k+1=0,
∴$\frac{|3k+1|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,∴k=-1或$\frac{1}{7}$,
∴直线l的方程为x-7y+8=0或x-y=0.
点评 本题主要考查求圆的标准方程,求出圆心的坐标,是解题的关键,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17.若关于x的不等式xa2-2xa-3<0在区间[-1,1]上恒成立,则实数a的取值范围是( )
| A. | [-1,1] | B. | [-1,3] | C. | (-1,1) | D. | (-1,3) |
15.已知函数f(x)满足:当f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^x}\\ f(x+1)\end{array}\right.{,^{\;}}$$\begin{array}{l}x≥4\\ \\ x<4\end{array}$,则f(2+log23)=( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
19.已知θ是△ABC的一个内角,且sinθ+cosθ=$\frac{3}{4}$,则方程x2sinθ-y2cosθ=1表示( )
| A. | 焦点在x轴上的双曲线 | B. | 焦点在y轴上的双曲线 | ||
| C. | 焦点在x轴上的椭圆 | D. | 焦点在y轴上的椭圆 |
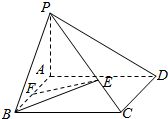 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.