题目内容
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DA,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DA,E,F分别是AB,PB的中点.(1)求证:CD⊥EF;
(2)当EF=
| 2 |
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)由线面垂直得PD⊥CD,由正方形性质,得CD⊥AD,从而CD⊥AP,由三角形中位线定理得EF∥AP.由此能证明CD⊥EF.
(2)由EF=
AP,且EF=
,得AP=2
,由△PAD为等腰直角三角形,得PD=AD=2,点F到底面ABCD的距离为
PD=1,由此能求出四棱锥F-ABCD的体积.
(2)由EF=
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
解答:
(1)证明:∵PD⊥底面ABCD,∴PD⊥CD…(2分)
∵底面ABCD为正方形,∴CD⊥AD,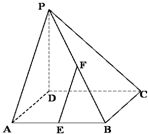
∴CD⊥平面PAD,从而CD⊥AP…(4分)
又E,F分别是AB,PB的中点,
∴EF∥AP.∴CD⊥EF…(6分)
(2)解:由(1)知,EF=
AP,且EF=
,
∴AP=2
…(8分)
又由题意知,△PAD为等腰直角三角形,∴PD=AD=2.
又∵点F为PB的中点,∴点F到底面ABCD的距离为
PD=1…(10分)
∴四棱锥F-ABCD的体积为V=
×2×2×1=
.…(12分)
∵底面ABCD为正方形,∴CD⊥AD,

∴CD⊥平面PAD,从而CD⊥AP…(4分)
又E,F分别是AB,PB的中点,
∴EF∥AP.∴CD⊥EF…(6分)
(2)解:由(1)知,EF=
| 1 |
| 2 |
| 2 |
∴AP=2
| 2 |
又由题意知,△PAD为等腰直角三角形,∴PD=AD=2.
又∵点F为PB的中点,∴点F到底面ABCD的距离为
| 1 |
| 2 |
∴四棱锥F-ABCD的体积为V=
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查异面直线垂直的证明,考查四棱锥的体积的求法,是中档题,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用.

练习册系列答案
相关题目
已知球O的直径为4,P,A,B,C为球面上四个点,P-ABC为正三棱锥,PA,PB,PC与平面ABC所成角均为60°则棱锥P-ABC体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某几何体的三视图如图所示,则它的体积是( )
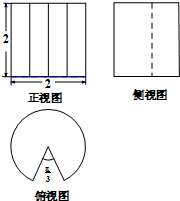

A、
| ||
B、
| ||
| C、π | ||
D、
|
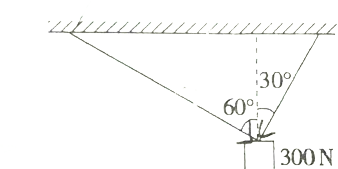 如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力.
如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力.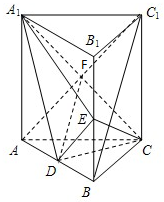 如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点. 设
设