题目内容
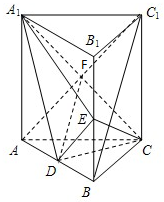 如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点.(1)证明:BC1∥平面A1CD
(2)若AA1=AC=CB=2,AB=2
| 2 |
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)根据线面平行的判定定理,需在平面A1DE内找一条与BC1平行的直线.因为ACC1A1是矩形,故对角线互相平分,所以连结AC1,与A1C交于点O.因为D是AB的中点,连结OD,则OD是△ABC1的中位线,所以BC1∥OD,从而可证得BC1∥平面A1CD.
(2)先求出CD⊥平面A1DE.再由VA1-CDE=VC-A1DE,利用等积法能三棱锥A1-CDE的体积.
(2)先求出CD⊥平面A1DE.再由VA1-CDE=VC-A1DE,利用等积法能三棱锥A1-CDE的体积.
解答:
(1)证明:连结AC1,交A1C于点O,连结OD,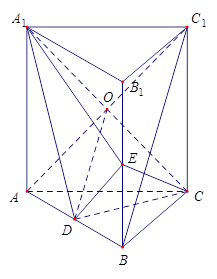
因为D是AB的中点,所以BC1∥OD,
因为BC1?平面A1CD,OD?平面A1CD,
所以BC1∥平面A1CD.
(2)解:因为AC=BC,D为AB的中点,所以CD⊥AB,
又因为该三棱柱是直三棱柱,所以CD⊥平面ABB1A1,
即CD⊥平面A1DE.
所以VA1-CDE=VC-A1DE=
×S△A1DE×CD.
因为AC=BC=2,AB=2
,所以CD=
.
S△A1DE=2
×2-
×
×2-
×
×1-
×2
×1=
,
所以VA1-CDE=VC-A1DE=
×
×
=1.

因为D是AB的中点,所以BC1∥OD,
因为BC1?平面A1CD,OD?平面A1CD,
所以BC1∥平面A1CD.
(2)解:因为AC=BC,D为AB的中点,所以CD⊥AB,
又因为该三棱柱是直三棱柱,所以CD⊥平面ABB1A1,
即CD⊥平面A1DE.
所以VA1-CDE=VC-A1DE=
| 1 |
| 3 |
因为AC=BC=2,AB=2
| 2 |
| 2 |
S△A1DE=2
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
所以VA1-CDE=VC-A1DE=
| 1 |
| 3 |
3
| ||
| 2 |
| 2 |
点评:本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
复数(3+2i)i等于( )
| A、-2+3i | B、-2-3i |
| C、2-3i | D、2+3i |
若集合A={x|1≤3x≤81},B={x|log2(x2-x)>1},则A∩B=( )
| A、(2,4] |
| B、[2,4] |
| C、(-∞,0)∪[0,4] |
| D、(-∞,-1)∪[0,4] |
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DA,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DA,E,F分别是AB,PB的中点.