题目内容
已知函数f(x)=x+alnx在x=1处的切线l与直线x+2y=0垂直,函数g(x)=f(x)+
x2-bx.
(Ⅰ)求实数a的值;
(Ⅱ)设x1,x2(x1<x2)是函数g(x)的两个极值点,若b≥
,求g(x1)-g(x2)的最小值.
| 1 |
| 2 |
(Ⅰ)求实数a的值;
(Ⅱ)设x1,x2(x1<x2)是函数g(x)的两个极值点,若b≥
| 7 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出函数的导数,利用切线与已知直线垂直,列出方程,即可求解a的值.
(Ⅱ)求出g'(x),列出求解函数的极值点的方程,利用韦达定理,化简g(x1)-g(x2),构造新函数,通过新函数的导数求解函数的最值.
(Ⅱ)求出g'(x),列出求解函数的极值点的方程,利用韦达定理,化简g(x1)-g(x2),构造新函数,通过新函数的导数求解函数的最值.
解答:
解:(Ⅰ)∵f(x)=x+alnx,
∴f′(x)=1+
,
又l与直线x+2y=0垂直,∴k=f′(1)=1+a=2,
∴a=1.
(Ⅱ) g′(x)=
+x-(b-1)=
,
令g′(x)=0,得x2-(b-1)x+1=0,∴x1+x2=b-1,x1x2=1,
∵g(x1)-g(x2)=[lnx1+
-(b-1)x1]-[lnx2+
-(b-1)x2]
=ln
+
(
-
)-(b-1)(x1-x2)=ln
-
(
-
),
∵0<x1<x2,所以设t=
(0<t<1),
h(t)=lnt-
(t-
)(0<t<1),
h′(t)=
-
(1+
)=-
<0,所以h(t)在(0,1)单调递减,
又b≥
, ∴(b-1)2≥
,
即(x1+x2)2=
=t+
+2≥
,
∵0<t<1, ∴4t2-17t+4≥0, ∴0<t≤
,
∴h(t)≥h(
)=
-2ln2,
故所求的最小值是
-2ln2.
∴f′(x)=1+
| a |
| x |
又l与直线x+2y=0垂直,∴k=f′(1)=1+a=2,
∴a=1.
(Ⅱ) g′(x)=
| 1 |
| x |
| x2-(b-1)x+1 |
| x |
令g′(x)=0,得x2-(b-1)x+1=0,∴x1+x2=b-1,x1x2=1,
∵g(x1)-g(x2)=[lnx1+
| 1 |
| 2 |
| x | 2 1 |
| 1 |
| 2 |
| x | 2 2 |
=ln
| x1 |
| x2 |
| 1 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| x1 |
| x2 |
| 1 |
| 2 |
| x1 |
| x2 |
| x2 |
| x1 |
∵0<x1<x2,所以设t=
| x1 |
| x2 |
h(t)=lnt-
| 1 |
| 2 |
| 1 |
| t |
h′(t)=
| 1 |
| t |
| 1 |
| 2 |
| 1 |
| t2 |
| (t-1)2 |
| 2t2 |
又b≥
| 7 |
| 2 |
| 25 |
| 4 |
即(x1+x2)2=
| (x1+x2)2 |
| x1•x2 |
| 1 |
| t |
| 25 |
| 4 |
∵0<t<1, ∴4t2-17t+4≥0, ∴0<t≤
| 1 |
| 4 |
∴h(t)≥h(
| 1 |
| 4 |
| 15 |
| 8 |
故所求的最小值是
| 15 |
| 8 |
点评:本题考查函数的导数的应用,函数的极值的求法韦达定理以及构造法的应用,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若P={y|y≥0},Q={x|-
≤x≤
},则P∩Q=( )
| 2 |
| 2 |
A、{0,
| ||||
| B、{(1,1),(-1,-1)} | ||||
C、[0,
| ||||
D、[-
|
 如图,在60°二面角的棱上有两点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,若AB=4,AC=6,BD=8,则线段CD的长为( )
如图,在60°二面角的棱上有两点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,若AB=4,AC=6,BD=8,则线段CD的长为( )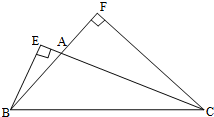 如图,BE、CF分别为钝角△ABC的两条高,已知AE=1,AB=3,CF=4
如图,BE、CF分别为钝角△ABC的两条高,已知AE=1,AB=3,CF=4