题目内容

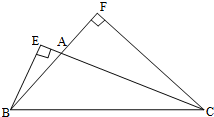如图，BE、CF分别为钝角△ABC的两条高，已知AE=1，AB=3，CF=4
2
，则BC边的长为
 
．
考点：相似三角形的性质
专题：选作题,立体几何
分析：先求出BE，再利用△BEA∽△CFA，求出AC，可得EC，利用勾股定理求出BC．
解答： 解：依题意，AE=1，AB=3，得BE=2
2
，
因△BEA∽△CFA得
AE
AF
=
BE
FC
=
AB
AC
，所以AF=2，AC=6，
所以EC=7，
所以BC=
BE2+EC2
=
57
．
故答案为：
57
．
点评：本题考查相似三角形的性质，考查学生的计算能力，正确运用相似三角形的性质是关键．
练习册系列答案
相关题目
已知x+y=-1，且x，y都是负实数，则xy+
1
xy
有（　　）
A、最小值2
B、最大值-2
C、最小值
17
4
D、最大值-
17
4
不等式组
5x+3y≤15
y≤x+1
x-5y≤3
表示的平面区域的面积为（　　）
A、7B、5C、3D、14
已知
a
=（
3
，1），
b
=（
3
，k），且
a
与
b
的夹角为
π
3
，则k=
 
．
已知函数f（x）=x+alnx在x=1处的切线l与直线x+2y=0垂直，函数g（x）=f（x）+
1
2
x2-bx．
（Ⅰ）求实数a的值；
（Ⅱ）设x1，x2（x1＜x2）是函数g（x）的两个极值点，若b≥
7
2
，求g（x1）-g（x2）的最小值．
已知三棱锥P-ABC的所有棱长都等于1，则三棱锥P-ABC的内切球的表面积
 
．
若△PAB是圆C：（x-2）2+（y-2）2=4的内接三角形，且PA=PB，∠APB=120°，则线段AB的中点的轨迹方程为（　　）
A、（x-2）2+（y-2）2=1
B、（x-2）2+（y-2）2=2
C、（x-2）2+（y-2）2=3
D、x2+y2=1
有好友来访，乘“车，船，飞机“的概率分别是
2
5
，
2
5
，
1
5
．乘三种工具迟到的概率分别是
1
3
，
1
4
，0．若来访好友迟到了，求好友来访乘船的概率是多少？
在△ABC中，AB=2，∠C=
π
4
，cos
B
2
=
2
5
5
，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网