题目内容
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、16 | ||
| D、32 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由已知中的三视图，我们可以判断出几何体的形状，进而求出几何体的底面面积和高后，代入棱锥体积公式，可得答案．
解答：
解：由已知中的三视图可得几何体是一个三棱锥，且棱锥的底面是一个以2底，以4为高的三角形
棱锥的高为4
故棱锥的体积V=
×
×2×4×4=
，
故选：A．
棱锥的高为4
故棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
故选：A．
点评：本题考查的知识点是由三视图求体积，其中根据已知判断出几何体的形状是解答本题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
定义域为R的偶函数f（x）满足对任意x∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-loga（|x|+1）在（0，+∞）上至少有三个零点，则a的取值范围是（ ）
A、（0，
| ||||
B、（
| ||||
C、（0，
| ||||
D、（
|
函数y=-ln（x+1）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
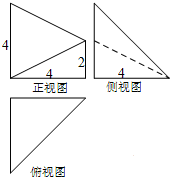已知某几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则此几何体的体积V=
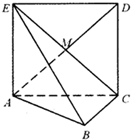如图，正方形 ACD E所在的平面与平面 A BC垂直，M是C E和 AD的交点，AC⊥BC，且 AC=BC．
如图根据下列三视图，想象物体原形，并画出物体的实物草图．