题目内容
已知函数y=
+
的单调递减区间是(
,6),则y的最大值是( )
| x-a |
| b-x |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:函数单调性的判断与证明
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:求出函数的定义域,将函数写成y═
,则y在(
,b)上递减,可得a,b,再由二次函数的最值,可得函数y的最大值.
b-a+2
|
| a+b |
| 2 |
解答:
解:由x-a≥0且b-x≥0,可得a≤x≤b,
则定义域为[a,b],
函数y=
+
=
=
,
则y在(
,b)上递减,
则有b=6,
=
,
解得a=-
,b=6.
则当x=
=
时,y取最大值,且为
+
=
.
故选D.
则定义域为[a,b],
函数y=
| x-a |
| b-x |
x-a+b-x+2
|
=
b-a+2
|
则y在(
| a+b |
| 2 |
则有b=6,
| a+b |
| 2 |
| 5 |
| 3 |
解得a=-
| 8 |
| 3 |
则当x=
| a+b |
| 2 |
| 5 |
| 3 |
|
6-
|
2
| ||
| 3 |
故选D.
点评:本题考查函数的单调区间,考查函数的最值的求法,考查运算能力,属于中档题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
设集合M={x|x≤-2或x≥4},CRN={X|2≤x≤6},则M∩N=( )
| A、(-∞,-2]∪(6,+∞) |
| B、(-∞,-2]∪(6,+∞) |
| C、(-∞,2)∪[4,+∞) |
| D、(-∞,2]∪[4,+∞) |
函数y=-ln(x+1)的图象大致是( )
A、 |
B、 |
C、 |
D、 |
已知函数f(x)=
在区间[1,3]上的最大值为A,最小值为B,则A+B=( )
| 2 |
| x |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
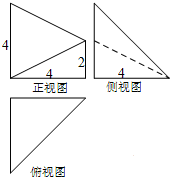 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V=
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V= 如图根据下列三视图,想象物体原形,并画出物体的实物草图.
如图根据下列三视图,想象物体原形,并画出物体的实物草图.