题目内容
数列{an}的通项公式an=
，则该数列的前99项之和等于 ．
| 1 | ||||
|
考点：数列的求和
专题：等差数列与等比数列
分析：由于an=
=
-
，利用“累加求和”即可得出．
| 1 | ||||
|
| n+1 |
| n |
解答：
解：∵an=
=
-
，
则该数列的前99项之和=(
-1)+(
-
)+…+(
-
)
=10-1
=9．
故答案为：9．
| 1 | ||||
|
| n+1 |
| n |
则该数列的前99项之和=(
| 2 |
| 3 |
| 2 |
| 100 |
| 99 |
=10-1
=9．
故答案为：9．
点评：本题考查了分母有理化、“累加求和”方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
若圆C的半径为1，点C与点（2，0）关于点（1，0）对称，则圆C的标准方程为（ ）
| A、x2+y2=1 |
| B、（x-3）2+y2=1 |
| C、（x-1）2+y2=1 |
| D、x2+（y-3）2=1 |
在如图所示的茎叶图中，甲、乙两组数据的中位数分别是f（x）=
+log4（x+1）的定义域是（ ）
| ||
| x-1 |
| A、（0，1）∪（1，4] |
| B、[-1，1）∪（1，4] |
| C、（-1，4） |
| D、（-1，1）∪（1，4] |
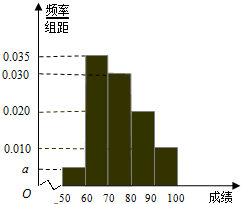某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：