题目内容
已知函数f(x)=Asin(ωx+ϕ)(A＞0，ω＞0，|ϕ|＜
)，
（1）若cos(ϕ+
)=-
，求ϕ的值；
（2）若f（x）最大值与最小值之差等于4，其相邻两条对称轴之间的距离等于
，求函数f（x）的解析式；
（3）在（2）的条件下，求最小正实数m，使f（x）图象向右平移m个单位对应的函数是偶函数（只需写出m的值，可不写步骤）
| π |
| 2 |
（1）若cos(ϕ+
| π |
| 2 |
| ||
| 2 |
（2）若f（x）最大值与最小值之差等于4，其相邻两条对称轴之间的距离等于
| π |
| 3 |
（3）在（2）的条件下，求最小正实数m，使f（x）图象向右平移m个单位对应的函数是偶函数（只需写出m的值，可不写步骤）
考点：函数y=Asin（ωx+φ）的图象变换,正弦函数的图象
专题：三角函数的求值
分析：（1）由条件利用诱导公式求得sinϕ 的值，结合|ϕ|＜
，可得ϕ=
．
（2）由f（x）=Asin（ωx+ϕ）的最大值与最小值之差等于4，可得A=2．再根据其相邻两条对称轴之间的距离等于
，求得ω=3，可得函数的解析式．
（3）根据函数y=Asin（ωx+φ）的图象变换规律可得y=2sin（3x+
-3m）为偶函数，可得
-3m=kπ+
，k∈z，由此可得m的最小正值．
| π |
| 2 |
| π |
| 4 |
（2）由f（x）=Asin（ωx+ϕ）的最大值与最小值之差等于4，可得A=2．再根据其相邻两条对称轴之间的距离等于
| π |
| 3 |
（3）根据函数y=Asin（ωx+φ）的图象变换规律可得y=2sin（3x+
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
解答：
解：（1）∵cos(ϕ+
)=-
=-sinϕ，∴sinϕ=
．
结合|ϕ|＜
，可得ϕ=
．
（2）由f（x）=Asin（ωx+ϕ）的最大值与最小值之差等于4，可得A=2．
再根据其相邻两条对称轴之间的距离等于
，可得
•
=
，求得ω=3．
故函数的解析式为 f(x)=2sin(3x+
)．
（3）由于f（x）图象向右平移m个单位对应的函数是y=2sin[3（x-m）+
]=2sin（3x+
-3m）为偶函数，
∴
-3m=kπ+
，k∈z，求得m=-
π-
，故当k=-1时，得到m的最小正值为
．
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
结合|ϕ|＜
| π |
| 2 |
| π |
| 4 |
（2）由f（x）=Asin（ωx+ϕ）的最大值与最小值之差等于4，可得A=2．
再根据其相邻两条对称轴之间的距离等于
| π |
| 3 |
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 3 |
故函数的解析式为 f(x)=2sin(3x+
| π |
| 4 |
（3）由于f（x）图象向右平移m个单位对应的函数是y=2sin[3（x-m）+
| π |
| 4 |
| π |
| 4 |
∴
| π |
| 4 |
| π |
| 2 |
| k |
| 3 |
| π |
| 12 |
| π |
| 4 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象变换规律，正弦函数、余弦函数的奇偶性，属于基础题．
练习册系列答案
相关题目
甲、乙两人进行乒乓球比赛，比赛规则为“3局2胜”，即以先赢2局者为胜．根据经验，每局比赛中甲获胜的概率为0.6，则本次比赛中甲以2：1的比分获胜的概率为（ ）
| A、0.288 |
| B、0.144 |
| C、0.432 |
| D、0.648 |
在△ABC中，已知
•
=tanA，当A=
时，△ABC的面积为（ ）
| AB |
| AC |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
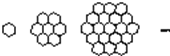蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂巢的截面图．其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，按此规律，以f（n）表示第n个图的蜂巢总数．