题目内容
11.设函数f(x)=|x+1|.(1)解不等式f(x)<2x;
(2)若2f(x)+|x-a|>8对任意x∈R恒成立,求实数a的取值范围.
分析 (1)去掉绝对值号,得到关于x的不等式组,解出即可;(2)问题转化为f(x)+|x-a|>3对任意x∈R恒成立,即|a+1|>3,解出即可.
解答 解:(1)由f(x)<2x,得:|x+1|<2x,
则-2x<x+1<2x,
即$\left\{\begin{array}{l}{x+1<2x}\\{x+1>-2x}\end{array}\right.$,解得:x>1,
故不等式的解集是(1,+∞);
(2)∵f(x)+|x-a|=|x+1|+|x-a|≥|x+1-x+a|=|a+1|,
又2f(x)+|x-a|>8=23对任意x∈R恒成立,
即f(x)+|x-a|>3对任意x∈R恒成立,
∴|a+1|>3,解得:a>2或a<-4,
故a的范围是(-∞,-4)∪(2,+∞).
点评 本题考查了解绝对值不等式问题,考查绝对值的性质,是一道中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1.下列函数为奇函数的是( )
| A. | y=x2+1 | B. | y=x3-2x | C. | y=2x+1 | D. | y=2x4+3x2 |
19.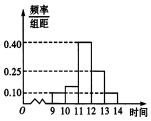 在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )
在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )
 在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )
在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )| A. | 3万元 | B. | 6万元 | C. | 8万元 | D. | 10万元 |
16.若复数z=$\frac{4-2ai}{1-i}$(a∈R)的实部为1,则z的虚部为( )
| A. | 1 | B. | 3 | C. | -1 | D. | -3 |
3.已知函数f(x)=-x2-6x-3,g(x)=$\frac{{e}^{x}+ex}{ex}$,实数m,n满足m<n<0,若?x1∈[m,n],?x2∈(0,+∞),使得f(x1)=g(x2)成立,则n-m的最大值为( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{5}$ |