题目内容
3.已知函数f(x)=-x2-6x-3,g(x)=$\frac{{e}^{x}+ex}{ex}$,实数m,n满足m<n<0,若?x1∈[m,n],?x2∈(0,+∞),使得f(x1)=g(x2)成立,则n-m的最大值为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{5}$ |
分析 利用导数法可得当x=1时,g(x)取最小值2,由f(x)=-x2-6x-3在x=-3时,取最大值6,令f(x)=2,则x=-5,或x=-1,数形结合可得答案.
解答 解:∵g(x)=$\frac{{e}^{x}+ex}{ex}$,
∴g′(x)=$\frac{{e}^{x}(x-1)}{e{x}^{2}}$,
当0<x<1时,g′(x)<0,g(x)为减函数,
当x>1时,g′(x)>0,g(x)为增函数,
故当x=1时,g(x)取最小值2,
由f(x)=-x2-6x-3在x=-3时,取最大值6,
令f(x)=2,则x=-5,或x=-1,
作两个函数的图象如图所示: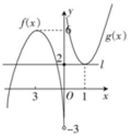
由图可得:n-m的最大值为-1-(-5)=4,
故选:A
点评 本题考查的知识点是利用导数研究函数的最值,二次函数的图象和性质,数形结合思想,难度中档.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
18.若实数x,y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$则z=-$\frac{5}{4x+3y}$的最大值为( )
| A. | -$\frac{15}{8}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{1}{2}$ | D. | -1 |
8.在等差数列{an}中,a1=3,2a2=a4,则a7等于( )
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
12.已知a>0,函数f(x)=x2+alnx-ax在(0,+∞)上是增函数,则a的最大值为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | 8 |
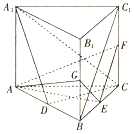 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F、G分别是BC、CC1、BB1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F、G分别是BC、CC1、BB1的中点.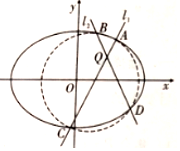 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.