题目内容
1.若复数z满足2+zi=z-2i(i为虚数单位),则复数z的模|z|=( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 利用复数的运算法则、模的计算公式即可得出.
解答 解:2+zi=z-2i(i为虚数单位),∴z(1-i)=2(1+i),
∴z(1-i)(1+i)=2(1+i)(1+i),
∴z=2i.
则复数z的模|z|=2.
故选:A.
点评 本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.设实数x,y满足$\left\{\begin{array}{l}x+y-6≥0\\ x+2y-14≤0\\ 2x+y-10≤0\end{array}\right.$,则2xy的最大值为( )
| A. | 25 | B. | 49 | C. | 12 | D. | 24 |
6.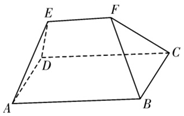 中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
 中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
13.已知抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l于点Q,M,N分别为PQ,PF的中点,MN与x轴相交于点R,若∠NRF=60°,则|FR|等于( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
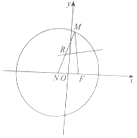 已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.
已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.