题目内容
16.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知b=$\frac{5}{8}$a,A=2B,则cosA=$\frac{7}{25}$.分析 由已知及正弦定理,二倍角的正弦函数公式化简可得cosB=$\frac{4}{5}$,进而利用二倍角的余弦函数公式即可计算得解.
解答 解:∵A=2B,
∴sinA=sin2B=2sinBcosB,
∵b=$\frac{5}{8}$a,
∴由正弦定理可得:$\frac{a}{b}=\frac{8}{5}$=$\frac{sinA}{sinB}$=$\frac{2sinBcosB}{sinB}$=2cosB,
∴cosB=$\frac{4}{5}$,
∴cosA=cos2B=2cos2B-1=$\frac{7}{25}$.
故答案为:$\frac{7}{25}$.
点评 本题主要考查了正弦定理,二倍角的正弦函数公式,二倍角的余弦函数公式在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
7.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完,若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领到的钱数不少于其他任何人)的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{4}$ |
4.为了得到函数y=4sinxcosx,x∈R的图象,只要把函数y=sin2x-$\sqrt{3}$cos2x,x∈R图象上所有的点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
11.某学校为了解本校学生的身体素质情况,决定在全校的1000名男生和800名女生中按分层抽样的方法抽取45名学生对他们课余参加体育锻炼时间进行问卷调查,将学生课余参加体育锻炼时间的情况分三类:A类(课余参加体育锻炼且平均每周参加体育锻炼的时间超过3小时),B类(课余参加体育锻炼但平均每周参加体育锻炼的时间不超过3小时),C类(课余不参加体育锻炼),调查结果如表:
(1)求出表中x、y的值;
(2)根据表格统计数据,完成下面的列联表,并判断是否有90%的把握认为课余参加体育锻炼且平均每周参加体育锻炼的时间超过3小时与性别有关;
(3)在抽取的样本中,从课余不参加体育锻炼学生中随机选取三人进一步了解情况,求选取三人中男女都有且男生比女生多的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| A类 | B类 | C类 | |
| 男生 | 18 | x | 3 |
| 女生 | 10 | 8 | y |
(2)根据表格统计数据,完成下面的列联表,并判断是否有90%的把握认为课余参加体育锻炼且平均每周参加体育锻炼的时间超过3小时与性别有关;
| 男生 | 女生 | 总计 | |
| A类 | |||
| B类和C类 | |||
| 总计 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
1.若复数z满足2+zi=z-2i(i为虚数单位),则复数z的模|z|=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
8.已知集合A={x|7<2x<33,x∈N},B={x|log3(x-1)<1},则A∩(∁RB)等于( )
| A. | {4,5} | B. | {3,4,5} | C. | {x|3≤x<4} | D. | {x|3≤x≤5} |
5.在平面直角坐标系xOy中,双曲线C的一个焦点为F(2,0),一条渐近线的倾斜角为60°,则C的标准方程为( )
| A. | $\frac{x^2}{3}-{y^2}=1$ | B. | $\frac{y^2}{3}-{x^2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | ${y^2}-\frac{x^2}{3}=1$ |
10.已知椭圆x2+2y2=1的左、右焦点分别为F1、F2,过椭圆上任意一点P作切线l,记F1、F2到l的距离分别为d1、d2,则d1•d2=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
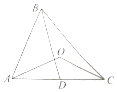 如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.
如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.