题目内容
14．若数列$\sqrt{2}$，$\sqrt{5}$，$2\sqrt{2}$，$\sqrt{11}$，$\sqrt{14}$，…，则$4\sqrt{2}$是这个数列的第（ ）项．| A． | 8 | B． | 9 | C． | 10 | D． | 11 |
分析 数列$\sqrt{2}$，$\sqrt{5}$，$2\sqrt{2}$，$\sqrt{11}$，$\sqrt{14}$，…，即数列$\sqrt{2}$，$\sqrt{5}$，$\sqrt{8}$，$\sqrt{11}$，$\sqrt{14}$，…，其被开方数成等差数列，利用通项公式即可得出．
解答 解：数列$\sqrt{2}$，$\sqrt{5}$，$2\sqrt{2}$，$\sqrt{11}$，$\sqrt{14}$，…，即数列$\sqrt{2}$，$\sqrt{5}$，$\sqrt{8}$，$\sqrt{11}$，$\sqrt{14}$，…，
其被开方数成等差数列，首项为2，公差为5-2=3．
∴an=2+3（n-1）=3n-1．
令3n-1=32，
解得n=11．
则$4\sqrt{2}$即$\sqrt{32}$是这个数列的第11项．
故选：D．
点评 本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
4．
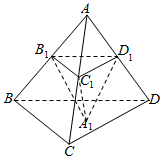如图，在棱长为a（a＞0）的正四面体ABCD中，点B1，C1，D1分别在棱AB，AC，AD上，且平面B1C1D1∥平面BCD，A1为△BCD内一点，记三棱锥A1-B1C1D1的体积V，设$\frac{A{D}_{1}}{AD}$=x，对于函数V=f（x），则（ ）
如图，在棱长为a（a＞0）的正四面体ABCD中，点B1，C1，D1分别在棱AB，AC，AD上，且平面B1C1D1∥平面BCD，A1为△BCD内一点，记三棱锥A1-B1C1D1的体积V，设$\frac{A{D}_{1}}{AD}$=x，对于函数V=f（x），则（ ）| A． | 当x=$\frac{2}{3}$时，函数f（x）取到最大值 | |
| B． | 函数f（x）在（$\frac{1}{2}$，1）上是减函数 | |
| C． | 函数f（x）的图象关于直线x=$\frac{1}{2}$对称 | |
| D． | 存在x0，使得f（x0）$＞\frac{1}{3}{V}_{A-BCD}$（其中VA-BCD为四面体ABCD的体积） |
2．设命题p：函数y=-xsinx的图象关于原点对称，
命题q：函数y=-xsinx在区间[0，$\frac{π}{2}$]上单调递减，
则下列命题中正确的是（ ）
命题q：函数y=-xsinx在区间[0，$\frac{π}{2}$]上单调递减，
则下列命题中正确的是（ ）
| A． | p∧q | B． | ￢p∧q | C． | p∨（￢q） | D． | （￢p）∧（￢q） |
9．某火锅店为了了解气温对营业额的影响，随机记录了该店1月份中5天的日营业额y（单位：千元）与该地当日最低气温x（单位：℃）的数据，如表：
（Ⅰ）求y关于x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
（Ⅱ）判定y与x之间是正相关还是负相关；若该地1月份某天的最低气温为6℃，用所求回归方程预测该店当日的营业额
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$．
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
（Ⅱ）判定y与x之间是正相关还是负相关；若该地1月份某天的最低气温为6℃，用所求回归方程预测该店当日的营业额
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$．
19．在△ABC中，角A、B、C所对的边分别为a、b、c．若c=3，$C=\frac{π}{3}$，且a+b=4，则△ABC的面积为（ ）
| A． | $\frac{7\sqrt{3}}{12}$ | B． | $\frac{7\sqrt{3}}{4}$ | C． | $\frac{7}{12}$ | D． | $\frac{5\sqrt{3}}{12}$ |
4．$\underset{lim}{n→∞}$$\sum_{i=1}^{n}$（$\frac{1}{n}$sin$\frac{i}{n}$）=（ ）
| A． | 1-cos1 | B． | 1-sin1 | C． | $\frac{π}{2}$ | D． | -$\frac{π}{2}$ |