题目内容
13.在平面直角坐标系内,直线l:2x+y-2=0,将l与两坐标轴围成的封闭图形绕y轴旋转一周,所得几何体的体积为$\frac{2}{3}π$.分析 由题意此几何体的体积可以看作是:V=${∫}_{0}^{2}π(\frac{y}{2}-1)^{2}dy$,求出积分即得所求体积,方法二由题意可得绕y轴旋转,形成的是以1为半径,2为高的圆锥,根据圆锥的体积公式,即可求得所得几何体的体积.
解答 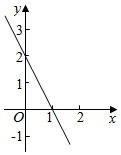 解:由题意可知:V=${∫}_{0}^{2}π(\frac{y}{2}-1)^{2}dy$,
解:由题意可知:V=${∫}_{0}^{2}π(\frac{y}{2}-1)^{2}dy$,
∴V=π($\frac{1}{12}$y3-$\frac{1}{2}{y}^{2}+y$) ${丨}_{0}^{2}$,
=$\frac{2π}{3}$.
方法二:由题意可知绕y轴旋转,形成的是以1为半径,2为高的圆锥,
则V=$\frac{1}{3}$•π×12×2=$\frac{2π}{3}$,
故答案为$\frac{2}{3}π$.
点评 本题考查用定积分求简单几何体的体积,求解的关键是找出被积函数来及积分区间,属于基础题.

练习册系列答案
相关题目
4.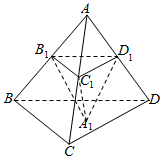 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )| A. | 当x=$\frac{2}{3}$时,函数f(x)取到最大值 | |
| B. | 函数f(x)在($\frac{1}{2}$,1)上是减函数 | |
| C. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| D. | 存在x0,使得f(x0)$>\frac{1}{3}{V}_{A-BCD}$(其中VA-BCD为四面体ABCD的体积) |
2.设命题p:函数y=-xsinx的图象关于原点对称,
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |