题目内容
已知函数f(x)＝ln(1＋x)－mx.
(1)求函数f(x)的极值；
(2)求证：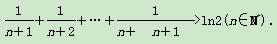
．
解 (1)对f(x)求导，得f′(x)＝
－m(x>－1)．
当m≤0时，f′(x)>0恒成立，则f(x)为
(－1，＋∞)上的增函数，所以f(x)没有极值．
当m>0时，由f′(x)>0，得－1<x<
－1；
由f′(x)<0，得x>－1.
所以f(x)在
上单调递增，
在
上单调递减．
故当x＝－1时，f(x)有极大值
，但无极小值．
(2)证明：取m＝1，由(1)知f(x)＝ln(1＋x)－x在(0，＋∞)上单调递减，所以f(x)<f(0)＝0.
即ln(1＋x)<x(x>0)．
令x＝
(k>0)，得ln(1＋)<，即ln
<，分别取k＝n＋1，n＋2，…，n＋(n＋1)，
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
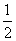x2＋4x－3lnx在[t，t＋1]上不单调，则t的取值范围是________．
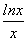，其中e是自然常数，a∈R.
；
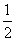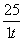(t的单位：s，v的单位：m/s)行驶至停止．在此期间汽车继续行驶的距离(单位：m)是( )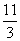
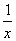＋2x＋2e2x，直线x＝1，x＝e和x轴所围成的区域的面积是________．
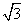(sin2x－cos2x)－2sinxcosx.
，求f(x)的单调递增区间．