题目内容
已知a,b∈R,t>0,下列四个条件中,使a>b成立的必要不充分条件是( )
| A、a>b-t |
| B、a>b+t |
| C、|a|>|b| |
| D、4a>4b |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据必要不充分条件的概念,只要看a>b能得到哪个选项,而由该选项得不到a>b即可.
解答:
解:使a>b成立的必要不充分条件,即a>b能得到哪个条件,而由该条件得不到a>b:
∵t>0,∴a>b时,能得到a>b-t,得不到a>b+t,得不到|a|>|b|,比如a=-2,b=-3;
而a>b能得到4a>4b,同样4a>4b能得到a>b;
∴A正确.
故选A.
∵t>0,∴a>b时,能得到a>b-t,得不到a>b+t,得不到|a|>|b|,比如a=-2,b=-3;
而a>b能得到4a>4b,同样4a>4b能得到a>b;
∴A正确.
故选A.
点评:考查必要条件、充分条件、必要不充分条件的概念,以及指数函数的单调性.

练习册系列答案
相关题目
某次国际象棋比赛规定,胜一局得3分,平一局得1分,负一局得0分,某参赛队员比赛一局胜的概率为a,平局的概率为b,负的概率为c(a、b、c∈[0,1)),已知他比赛一局得分的数学期望为1,则ab的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若3a>1,则实数a的取值范围为( )
| A、a<0 | B、0<a<1 |
| C、a>0 | D、a>2 |
函数f(x)=2x-x2在区间(0,3)上的最大值、最小值分别为( )
| A、1,-3 |
| B、0,-3 |
| C、无最大值,-3 |
| D、1,无最小值 |
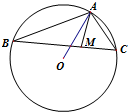 如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足
如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足| BM |
| MC |
| AM |
| AO |
| A、21 | B、22 | C、29 | D、36 |