题目内容
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:
①若m∥α,n∥α,m∥β,n∥β,则α∥β;
②若α⊥γ,β⊥γ,α∩β=m,n⊂γ,则m⊥n;
③若m⊥α,α⊥β,m∥n,则n∥β;
④若n∥α,n∥β,α∩β=m,那么m∥n.
其中正确命题的序号是________.
②④
[解析] 命题①中,直线m、n不一定相交,即命题①不正确;命题②中,垂直于同一个平面的两个平面的位置关系可以平行或相交,若相交,其交线必与第三个平面垂直,∴m⊥γ,又n⊂γ,∴m⊥n,即命题②正确;若m∥n,m⊥α,则n⊥α,又α⊥β,则n∥β或n⊂β,即命题③不正确;由线面平行的判定与性质定理可知命题④正确.则正确命题的序号为②④.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
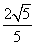 ≤t≤2
≤t≤2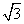 } B.{t|
} B.{t|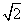 }
}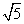 ,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,△AMC1的面积为________.
,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,△AMC1的面积为________.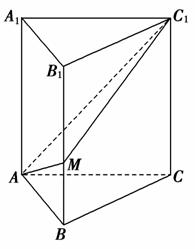
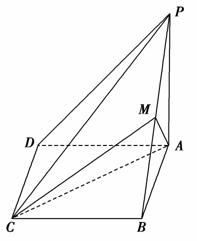
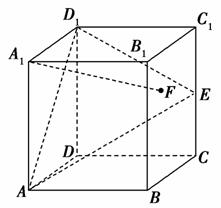
 ,AA1=3,E为CD上一点,DE=1,EC=3.
,AA1=3,E为CD上一点,DE=1,EC=3.