题目内容
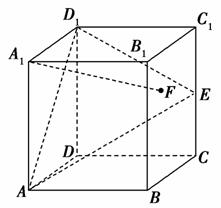
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是正方形BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( )
A.{t|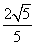 ≤t≤2
≤t≤2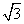 } B.{t|
} B.{t|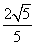 ≤t≤2}
≤t≤2}
C.{t|2≤t≤2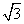 } D.{t|2≤t≤2
} D.{t|2≤t≤2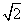 }
}
D
[解析] 如图,设M、N分别是B1C1、BB1的中点,连接A1M、A1N、MN,根据正方体的性质易知,平面A1MN∥平面AED1,又A1F∥平面AED1,所以A1F⊂平面A1MN,所以点F必在线段MN上移动.连接B1F,因为A1B1⊥平面BCC1B1,所以直线A1F与平面BCC1B1所成的角即为∠B1FA1,即t= ,当t最大时,点F位于MN的中点,t最小时,点F位于M点或N点.易求得最大角的正切值为2
,当t最大时,点F位于MN的中点,t最小时,点F位于M点或N点.易求得最大角的正切值为2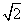 ,最小角的正切值为2,故选D.
,最小角的正切值为2,故选D.


练习册系列答案
相关题目
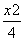 -y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是________.
-y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是________. 的值为( )
的值为( ) a2
a2 a2 D.
a2 D. a2
a2
 B.
B.
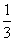 D.
D.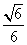
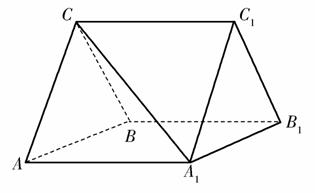
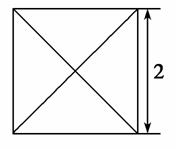
 ) D.4
) D.4
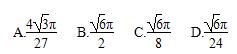
 π,则这个直三棱柱的体积等于( )
π,则这个直三棱柱的体积等于( )